选择搜索算法 Selective Search
原论文:
关键字:分层分组算法、初始化区域集、相似度计算
keywords: Hierarchical Grouping Algorithm, Obtaining Initial Regions, Calculating Similarity
分层分组算法 Hierarchical Grouping Algorithm
selective search的主要内容。
Input: (color) image
Output: Set of object location hypotheses L
Obtain initial regions $R = {r_1, \ldots, r_n}$ using Graph-Based Image Segmentation
Initialise similarity set $S = \Phi$
foreach Neighbouring region pair $(r_i, r_j)$ do
Calculate similarity $s(r_i, r_j)$
$S = S \cup s(r_i, r_j)$
while $S \neq \Phi$ do
Get highest similarity $s(r_i, r_j) = \mathbf{max}(S)$
Merge corresponding regions $r_t = r_i \cup r_j$
Remove similarities regarding $r_i : S \setminus s(r_i, r_*)$
Remove similarities regarding $r_i : S \setminus s(r_*, r_j)$
Calculate similarity set $S_t$ between $r_t$ and its neighbours
$S = S \cup S_t$
$R = R\cup r_t$
Extract object location boxes $L$ from all regions in $R$
算法具体解释
- 使用 Efficient Graph-Based Image Segmentation 中的方法初始化区域集 $R$;
- 计算 $R$ 中相邻区域的相似度,并以此构建相似度集 $S$;
- 如果 $S$ 不为空,则执行以下7个子步骤,否则,跳至步骤4;
- 获取 $S$ 中的最大值 $s( r_i, r_j )$;
- 将 $r_i$ 与 $r_j$ 合并成一个新的区域 $r_t$;
- 将 $S$ 中与 $r_i$ 有关的值 $s(r_i, r_*)$ 剔除掉;
- 将 $S$ 中与 $r_j$ 有关的值 $s(r_*, r_j)$ 剔除掉;
- 使用步骤2中的方法,构建 $S_t$,它是 $S$ 的元素与 $r_t$ 之间的相似度构成的集合;
- 将 $S_t$ 中的元素全部添加到 $S$ 中;
- 将 $r_t$ 放入 $R$ 中。
- 将 $R$ 中的区域作为目标的位置框 $L$,这就是算法的执行结果。
相似度计算
原论文里考虑了四个方面的相似度:颜色 $s_{colour}$ 、纹理 $s_{texture}$ 、尺度 $s_{size}$ 、空间交叠 $s_{fill}$ ,并将这四个相似度以线性组合的方式综合在一起,作为最终被使用的相似度 $s(r_i,r_j)$:
\[s(r_i,r_j)=\alpha_1 s_{colour}(r_i,r_j) + \alpha_2 s_{texture}(r_i,r_j) + \alpha_3 s_{size}(r_i,r_j) + \alpha_4 s_{fill}(r_i,r_j)\]下面是这四种相似度的介绍。
颜色相似度
将区域的颜色空间转换为直方图,三个颜色通道的bins取25。于是我们可以得到某个区域 $r_i$ 的颜色直方图向量:$C_i={c^1i,…,c^n_i}$,其中 $n=75$(计算方式:$bins\times n{channels}=25\times3$),并且$C_i$是用区域的 $L_1$ 范数归一化后的向量。关于 $r_t = r_i \cup r_j$ 的 $C_t$,计算方式是这样的:
\[C_t=\frac{size(r_i)\times C_i + size(r_j)\times C_j}{size(r_i)+size(r_j)}\]而 $r_t$ 尺寸的计算方式为:$size(r_t)=size(r_i)+size(r_j)$。 颜色相似度的计算公式:
\[s_{colour}(r_i,r_j)=\sum^{n}_{k=1}\textbf{min}(c^k_i,c^k_j)\]纹理相似度
对每一个颜色通道,在8个方向上提取高斯导数 $\sigma=1$。在每个颜色通道的每个方向上,提取一个bins为10的直方图,从而得到每个区域 $r_i$ 的纹理直方图向量 $T_i={t^1i,…,t^n_i}$,其中 $n=240$(计算方式:$n{orientations}\times bins\times n_{channels}=8\times10\times3$),$T_i$ 也是用区域的 $L_1$ 范数归一化后的向量。 纹理相似度的计算公式:
\[s_{texture}(r_i,r_j)=\sum^{n}_{k=1}\mathbf{min}(t^k_i,t^k_j)\]尺度相似度
尺度相似度的计算公式: 用于优先合并小区域。
\[s_{size}(r_i,r_j)=1-\frac{size(r_i)+size(r_j)}{size(im)}\]其中,$size(im)$是整张图片的像素级的尺寸。
空间交叠相似度
用于优先合并被包含进其他区域的区域。 空间交叠相似度的计算公式:
\[s_{fill}(r_i,r_j)=1-\frac{size(BB_{ij})-size(r_i)-size(r_j)}{size(im)}\]其中,$BB_{ij}$ 是能够框住 $r_i$ 与 $r_j$ 的最小矩形框。
基于图的图像分割 Graph-Based Image Segmentation
介绍
基于图的图像分割(Graph-Based Image Segmentation),论文《Efficient Graph-Based Image Segmentation》,P. Felzenszwalb, D. Huttenlocher,International Journal of Computer Vision, Vol. 59, No. 2, September 2004
论文下载和论文提供的C++代码在这里。
Graph-Based Segmentation是经典的图像分割算法,其作者Felzenszwalb也是提出DPM(Deformable Parts Model)算法的大牛。
Graph-Based Segmentation算法是基于图的贪心聚类算法,实现简单,速度比较快,精度也还行。不过,目前直接用它做分割的应该比较少,很多算法用它作垫脚石,比如Object Propose的开山之作《Segmentation as Selective Search for Object Recognition》就用它来产生过分割(over segmentation)。
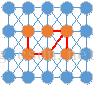
论文中,初始化时每一个像素点都是一个顶点,然后逐渐合并得到一个区域,确切地说是连接这个区域中的像素点的一个MST(最小生成树)。如下图,棕色圆圈为顶点,线段为边,合并棕色顶点所生成的MST,对应的就是一个分割区域。分割后的结果其实就是森林。
相似性
既然是聚类算法,那应该依据何种规则判定何时该合二为一,何时该继续划清界限呢?对于孤立的两个像素点,所不同的是灰度值,自然就用灰度的距离来衡量两点的相似性,本文中是使用RGB的距离,即
当然也可以用perceptually uniform的Luv或者Lab色彩空间,对于灰度图像就只能使用亮度值了,此外,还可以先使用纹理特征滤波,再计算距离,比如先做Census Transform再计算Hamming distance距离。
全局阈值 » 自适应阈值,区域的类内差异、类间差异
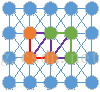
上面提到应该用亮度值之差来衡量两个像素点之间的差异性。对于两个区域(子图)或者一个区域和一个像素点的相似性,最简单的方法即只考虑连接二者的边的不相似度。如下图,已经形成了棕色和绿色两个区域,现在通过紫色边来判断这两个区域是否合并。那么我们就可以设定一个阈值,当两个像素之间的差异(即不相似度)小于该值时,合二为一。迭代合并,最终就会合并成一个个区域,效果类似于区域生长:星星之火,可以燎原。
举例说明:

对于上右图,显然应该聚成上左图所示的3类:高频区h,斜坡区s,平坦区p。
如果我们设置一个全局阈值,那么如果h区要合并成一块的话,那么该阈值要选很大,但是那样就会把p和s区域也包含进来,分割结果太粗。如果以p为参考,那么阈值应该选特别小的值,那样的话p区是会合并成一块,但是h区就会合并成特别特别多的小块,如同一面支离破碎的镜子,分割结果太细。显然,全局阈值并不合适,那么自然就得用自适应阈值。对于p区该阈值要特别小,s区稍大,h区巨大。
先来两个定义,原文依据这两个附加信息来得到自适应阈值。 一个区域内的类内差异 $\mathrm{Int}(C)$:
可以近似理解为一个区域内部最大的亮度差异值,定义是MST中不相似度最大的一条边。 俩个区域的类间差异 $\mathrm{Diff}(C1, C2)$:
即连接两个区域所有边中,不相似度最小的边的不相似度,也就是两个区域最相似的地方的不相似度。
直观的判断,当:
\[\mathrm{Int}(C) \geq \mathrm{Diff}(C1, C2)\]时,两个区域应当合并。
算法步骤
- 计算每一个像素点与其8邻域或4邻域的不相似度;
- 将边按照不相似度non-decreasing排列(从小到大)排序得到e1, e2, …, en;
- 选择ei;
- 对当前选择的边ej(vi和vj不属于一个区域)进行合并判断。设其所连接的顶点为(vi, vj),
- if 不相似度小于二者内部不相似度
- 更新阈值以及类标号
- else
- 则按照排好的顺序,选择下一条边转到 Step 4,否则结束。
边界框回归 Bounding-Box Regression
简介
相比传统的图像分类,目标检测不仅要实现目标的分类,而且还要解决目标的定位问题,即获取目标在原始图像中的位置信息。在不管是最初版本的RCNN,还之后的改进版本——Fast RCNN和Faster RCNN都需要利用边界框回归来预测物体的目标检测框。因此掌握边界框回归(Bounding-Box Regression)是极其重要的,这是熟练使用RCNN系列模型的关键一步,也是代码实现中比较重要的一个模块。接下来,我们对边界框回归(Bounding-Box Regression)进行详细介绍。
首先我们对边界框回归的输入数据集进行说明。输入到边界框回归的数据集为 ${P^i, G^i}_{i=1,\cdots,N}$,其中 $P^i = (P^i_x, P^i_y, P^i_w, P^i_h)$,$G^i = (G_x^i, G^i_y, G^i_w, G^i_h)$。$P^i$ 代表第 $i$ 个带预测的候选目标检测框即 region proposal。$G^i$ 是第 $i$ 个真实目标检测框即 ground-truth。在RCNN和Fast RCNN中, $P^i$是利用选择性搜索算法进行获取;Faster RCNN中, $P^i$是利用 RPN(Region Proposal Network,区域生成网络)获取。在$P^i$中, $P_x^i$ 代表候选目标框的中心点在原始图像中的 $x$ 坐标, $P^i_y$ 代表候选目标框的中心点在原始图像中的 $y$ 坐标, $P_w^i$ 代表候选目标框的长度, $P^i_h$ 代表候选目标框的宽度。 $G^i$ 的四维特征的含义与 $P^i$的一样。
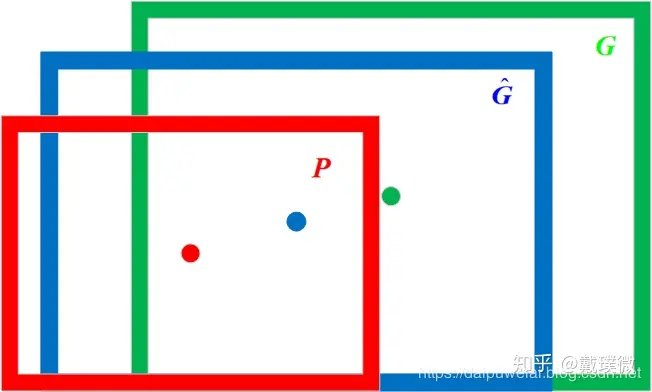
那么边界框回归所要做的就是利用某种映射关系,使得候选目标框(region proposal)的映射目标框无限接近于真实目标框(ground-truth)。将上述原理利用数学符号表示如下:在给定一组候选目标框 $P=(P_x, P_y, P_w, P_h)$ ,寻找到一个映射 $f$,使得 $f(P_x, P_y, P_w, P_h) = (\hat{G_x}, \hat{G_y}, \hat{G_w}, \hat{G_h}) \approx (G_x, G_y, G_w, G_h)$ 。边界框回归过程图像表示如下图所示。在图1中红色框代表候选目标框,绿色框代表真实目标框,蓝色框代表边界框回归算法预测目标框,红色圆圈代表选候选目标框的中心点,绿色圆圈代表选真实目标框的中心点,蓝色圆圈代表选边界框回归算法预测目标框的中心点。
算法细节
RCNN论文里指出,边界框回归是利用平移变换和尺度变换来实现映射 。平移变换的计算公式如下:
\[\left\{\begin{matrix} \hat{G_x} = P_wd_x(P)+P_x \\ \hat{G_y} = P_hd_y(P)+P_y \end{matrix}\right.\]尺度变换的计算公式如下:
\[\left\{\begin{matrix} \hat{G_w} = P_w\mathrm{exp}(d_w(P)) \\ \hat{G_h} = P_h\mathrm{exp}(d_h(P)) \end{matrix}\right.\]接下来要做的就是求解这4个变换($d_x, d_y, d_w, d_h$)。在边界框回归中,我们利用了线性回归在RCNN论文代表这AlexNet第5个池化层得到的特征即将送入全连接层的输入特征的线型函数。在这里,我们将特征记作 $\phi_5(P)$,那么 $d_(P)=w_^T\phi_5(P)$。因此,我们可以利用最小二乘法或者梯度下降算法进行求解 ,RCNN论文中给出了 的求解表达式:
\[w_* = \underset{\hat{w_*}}{\mathrm{arg}\,\mathrm{min}}\sum^N_{i=1}(t^i_*-\hat{w_*}\phi_5(P^i))^2 + \lambda\left \| \hat{w_*} \right \|^2\]其中:
\[\left\{\begin{matrix} t_x = \frac{G_x-P_x}{P_w} \\ t_y = \frac{G_y-P_y}{P_h} \\ t_w = \log\frac{G_w}{P_w} \\ t_h = \log\frac{G_h}{P_h} \end{matrix}\right.\]可以看出,上述模型就是一个Ridge回归模型。在RCNN中,边界框回归要设计4个不同的Ridge回归模型分别求解$w_x, w_y, w_w, w_h$。
模型细节
为什么x,y坐标要除以宽和高?
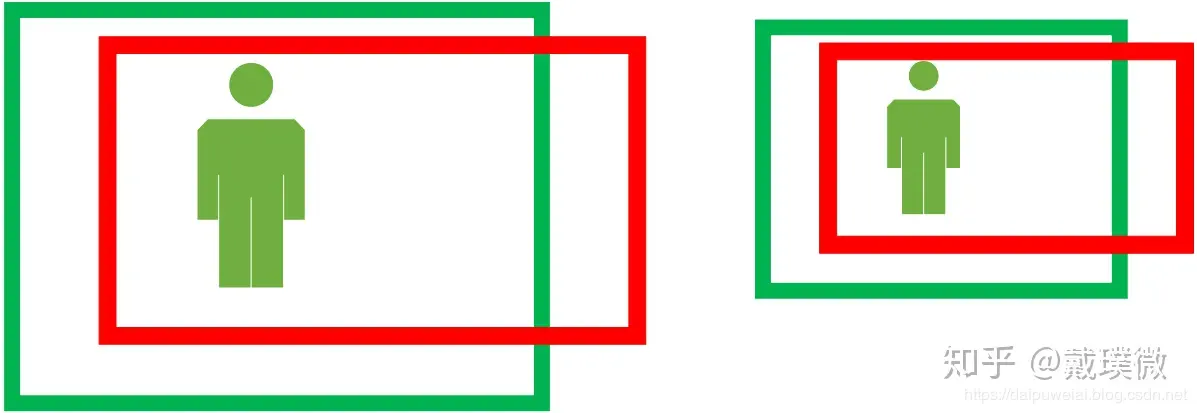
注意CNN有尺度不变性[来源?]。我们假设两张尺寸不同,但内容相同的图像。由于尺寸的变化,候选目标框和真实目标框坐标之间的偏移量也随着尺寸而成比例缩放,即这个比例值是恒定不变的。如果我们直接学习坐标差值,同一个x对应多个y,这明显不满足函数的定义。边框回归学习的是回归函数,然而你的目标却不满足函数定义,当然学习不到什么。
同时使用相对偏移量的好处可以自由选择输入图像的尺寸,使得模型灵活多变。也就说,对坐标偏移量除以宽高就是在做尺度归一化。
为什么宽高比要取对数?
我们想要得到一个放缩的尺度,也就是说这里限制尺度必须大于0。我们学习的怎么保证满足大于0呢?直观的想法就是EXP函数。
为什么loU较大时边界框回归可视为线性变换?
\[\lim_{x\to 0}\frac{\log(1+x)}{x}=1\]故
\[t_w = \log \frac{G_w}{P_w} = \log \left(1+\frac{G_w-P_w}{P_w}\right)\] \[t_h = \log \frac{G_h}{P_h} = \log \left(1+\frac{G_h-P_h}{P_h}\right)\]$G_w \approx P_w$ 和 $G_h \approx P_h$ 时选目标框和真实目标框非常接近,即IoU值较大。按照RCNN论文的说法,IoU大于0.6时,边界框回归可视为线性变换。
