残差网络 ResNet
残差网络是一个基础概念。
残差操作这一思想起源于论文《Deep Residual Learning for Image Recognition》。如果存在某个$K$层的网络$f$是当前最优的网络,那么可以构造一个更深的网络,其最后几层仅是该网络$f$第$K$层输出的恒等映射(Identity Mapping),就可以取得与$f$一致的结果;也许$K$还不是所谓“最佳层数”,那么更深的网络就可以取得更好的结果。总而言之,与浅层网络相比,更深的网络的表现不应该更差。但是更深的网络在训练过程中的难度更大,因此作者提出了残差网络的思想。
残差网络的定义
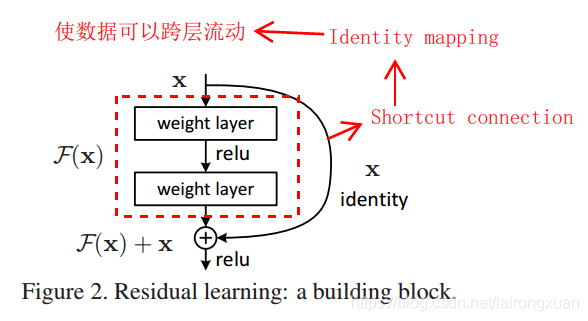
残差网络依旧让非线形层满足 $\mathcal{F}(x, w_h)$,然后从输入直接引入一个短连接到非线形层的输出上,使得整个映射变为
\[y = \mathcal{F}(x, w_h) + x\]这就是残差网路的核心公式,换句话说,残差是网络搭建的一种操作,任何使用了这种操作的网络都可以称之为残差网络。
训练网络的最终目的就是找到一组权重$w^\prime$,使 $F^\prime(x,w^\prime)$ 最逼近真实的函数 $H(x)$,用式子可表示为 $F^\prime(x,w^\prime) \to H(x)$。但是现实生活中,真实的函数 $H(x)$ 往往非常复杂,想要找到一个足够逼近的函数 $F^\prime(x,w^\prime)$ 比较困难,所花费的代价也较大,作者另辟蹊径减小了工作量。
作者的思路是引入恒等映射。如图所示,网络的输入依然还是 $x$,网络在输出之前还叠加了一次输入$x$,网络结构发生了变化,$w^\prime$ 变成了 $w$,$F^\prime(x,w^\prime)$ 变成了 $F(x,w)$。训练网络的目的也发生了改变,变成了找到一组权重 $w$ 使得 $F(x,w) +x \to H(x)$,即 $F(x,w) \to H(x) - x$。如果 $F(x,w)$ 的所有权重都为0,则网络就是恒等映射。
问题
引入残差为何可以更好的训练?
残差的思想都是去掉相同的主体部分,从而突出微小的变化,引入残差后的映射对输出的变化更敏感。
假设:在引入残差之前,输入 $x=6$,要拟合的函数 $H(x)=6.1$,也就是说平原网络找到了一组 $w^\prime$ 使得 $F^\prime (x,w^\prime) \to H(x)$。引入残差后,输入不变还是 $x=6$,要拟合的函数 $H(x)=6.1$,变化的是 $F(x,w)+x \to H(x))=6.1$,可得 $F(x,w) \to 0.1$。
如果需拟合的函数 $H(x)$ 增大了0.1,那么对平原网络来说 $F^\prime (x,w^\prime)$ 就是从6.1变成了6.2,增大了1.6%。而对于ResNet来说,$F(x,w)$ 从0.1变成了0.2,增大了100%。很明显,在残差网络中输出的变化对权重的调整影响更大,也就是说反向传播的梯度值更大,训练就更加容易。
ResNet如何解决梯度消失问题?
我们想象这么一个ResNet,它由 $L$ 个residual block组成,即多个如上图所示的单元构成。每一个单元的输入和输出表示为 $x_l$ 和 $x_{l+1}$ 。那么我们可得如下公式:
\[y_L = h(x_L) + F(x_L, w_L) = w_sx_L + F(x_L, w_L)\] \[x_{L+1} = f(y_L)\]注意,有两个假设:1. $x_{L+1} = f(y_L) = y_L$,2. $w_s = I$,即$w_s$为单位矩阵(恒等映射)。所以有
\[\begin{aligned}x_L & = X_{L-1} + F(x_{L-1}, w_{L-1}) \\ & = x_0 +\sum^{L-1}_{i=0}F(x_i, w_i) \\ & = x_l + \sum^{L-1}_{i=l}F(x_i, w_i) \end{aligned}\]在反向传播过程中,令$E$为总误差,有以下求导过程:
\[\frac{\partial E}{\partial x_l} = \frac{\partial E}{\partial x_L}\cdot\frac{\partial x_L}{\partial x_l}\left(x_l+\sum^{L-1}_{i=l}F(x_i, w_i)\right)\] \[=\frac{\partial E}{\partial x_L}\left(1+\sum^{L-1}_{i=l}\frac{\partial}{\partial x_l}F(x_i, w_i)\right)\]式子的第一个因子$\frac{\partial E}{\partial x_L}$表示的损失函数到达 L 的梯度,小括号中的1表明短路机制可以无损地传播梯度,而另外一项残差梯度则需要经过带有权重的层,梯度不是直接传递过来的。很显然,造成梯度消失的根本原因——梯度连乘不复存在了。残差梯度不会那么巧全为-1,而且就算其比较小,有1的存在也不会导致梯度消失。
需要注意,上述两个假设是必不可少的,否则如上关系不再成立。论文中提到,经实践证明,令 $w_s = I$ 是最优的选择。
Covolutional Neural Network (CNN)
万物起源。
引用一个比较直观的视频:
一个卷积神经网络主要由以下5层组成:
- 数据输入层/ Input layer
- 卷积计算层/ CONV layer
- ReLU激励层 / ReLU layer
- 池化层 / Pooling layer
- 全连接层 / FC layer
数据输入层
该层要做的处理主要是对原始图像数据进行预处理,其中包括:
- 去均值:把输入数据各个维度都中心化为0;
- 归一化:幅度归一化到同样的范围;
- PCA/白化:用PCA降维;白化是对数据各个特征轴上的幅度归一化
卷积计算层
描述卷积的四个量 一个卷积层的配置由如下四个量确定。
- 滤波器个数。使用一个滤波器对输入进行卷积会得到一个二维的特征图(feature map)。我们可以用时使用多个滤波器对输入进行卷积,以得到多个特征图。
- 感受野(receptive field) F,即滤波器空间局部连接大小(卷积核尺寸)。
- 零填补(zero-padding) P。随着卷积的进行,图像大小将缩小,图像边缘的信息将逐渐丢失。因此,在卷积前,我们在图像上下左右填补一些0,使得我们可以控制输出特征图的大小。
- 步长(stride) S。滤波器在输入每移动S个位置计算一个输出神经元。
应该使用多大的滤波器 尽量使用小的滤波器,如3×3卷积。通过堆叠多层3×3卷积,可以取得与大滤波器相同的感受野,例如三层3×3卷积等效于一层7×7卷积的感受野。但使用小滤波器有以下两点好处。
- 更少的参数量。假设通道数为D,三层3×3卷积的参数量为3×(D×D×3×3)=27D^2, 而一层7×7卷积的参数量为D×D×7×7=49D^2。
- 更多非线性。由于每层卷积层后都有非线性激活函数,三层3×3卷积一共经过三次非线性激活函数,而一层7×7卷积只经过一次。
1×1卷积 旨在对每个空间位置的D维向量做一个相同的线性变换。通常用于增加非线性,或降维,这相当于在通道数方向上进行了压缩。1×1卷积是减少网络计算量和参数的重要方式。
ROI: ROI pooling, ROI align, ROI wrap
ROI 是 Region of Interest 的缩写。
ROI Pooling
感兴趣区域池化是用于目标检测任务的神经网络层。它最初是由Ross Girshick在2015年4月提出的。
输入:
- 从具有多个卷积和最大池层的深度卷积网络获得的固定大小的feature map;
- 表示感兴趣区域列表的N×5矩阵,其中N是RoI的数量。第一列表示图像索引,其余四列是区域左上角和右下角的坐标。
对于每个ROI,它将其缩放到某个预定义的大小。缩放通过以下方式完成:
- 将区域提案划分为相等大小的部分(其数量与输出的维度相同)
- 找到每个部分的最大值
- 将这些最大值复制到输出(max pooling)
动画:
其实就是普通池化,只不过是对ROI做这些事情而已。
ROI Align
首先,feature map的大小并不是和原图像素数量等同,而是会被缩小。同时,在刚才的ROI Pooling步骤,经历了一个量化步骤——因为ROI的横纵尺寸是按照图片像素来的,边界不一定恰好在feature map的边界。那么就要对ROI的尺寸按照feature map每一“格”的分布进行取整。这样一来,一定会丢失信息。ROI Align就是解决了这个问题。
这里省略详细的计算内容。简要概括:
首先把feature map上的Rol切分成和pooling size要求等同的几个boxes。例如pooling layer size是$3 \times 3$,就把ROLI分割为 $3 \times 3$ 。
对于每一个box,创建四个采样点,分别是这个box $3\times 3$ 分割后内侧的四个分割线交点。
对于每个点,根据点周围四个feature map格子坐标中点计算双线性插值。
之后对这四个点获取最大值进行Pooling。
这样所有的数据就都用上了,会更加准确。
Region Proposal Network (RPN)
经典的检测方法生成检测框都非常耗时,Faster-RCNN 直接使用 RPN 生成检测框,能极大提升检测框的生成速度。RPN (Region Proposal Network) 用于生成候选区域(Region Proposal)。
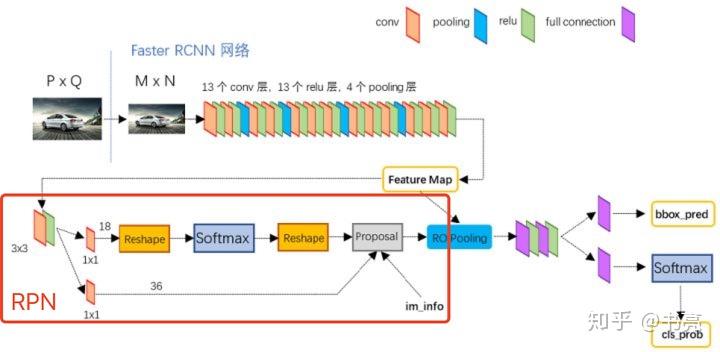
首先,CNN获得feature map;
接着,根据feature map的大小生成一大堆anchor,作为proposal的候选。
“RPN依靠在共享特征图上一个滑动的窗口,为每个位置生成9种目标框(anchor)。这9种anchor面积是128×128、256×256、512×512,长宽比是1:1、1:2、2:1,面积和长宽比两两组合形成9种anchor。”
例如,$40 \times 60$ 大小的feature map,总$anchor$数为 $40 \times 60 \times 9 \approx 20000$
获得如此多的候选者之后,再进行筛选:
判断物体还是背景,论文通过非极大值抑制(nms)的方法,设定IoU为0.7的阈值,即仅保留覆盖率不超过0.7的局部最大分数的box(粗筛)。最后留下大约2000个anchor,然后再取前N个box(比如300个)给Fast-RCNN。该文章的理解是IOU(与真值的交并比)>0.7为物体,即为正样本,IOU<0.3为背景,即为负样本。论文中RPN网络训练的时候,只使用了上述两类,与真值框的IoU介于0.3和0.7的anchor没有使用。
坐标修正,即回归问题,也就是找到原anchor到真值框的映射关系,可以通过平移和缩放实现,当anchor和真值框比较接近时,认为这种变换是一种线性变换,可以使用线性回归模型进行微调(边界框回归)。在得到每一个候选区域anchor的修正参数之后,我们就可以计算出精确的anchor,然后按照物体的区域得分从大到小对得到的anchor排序,然后提出一些宽或者高很小的anchor(获取其它过滤条件),再经过非极大值抑制抑制,取前Top-N的anchors,然后作为proposals(候选框)输出,送入到RoI Pooling层。
Spatial Pyramid Pooling (SPP)
SPP也是Fast R-CNN采用了的。详见文章Spatial Pyramid Pooling in Deep Convolutional Networks for Visual Recognition
当尺寸大小不同的图像输入到相同的多层卷积网络中,得到的feature map大小是不同的,数量是相同(相同的filters)。
对一个固定的CNN,全连接层的输入是一个固定的数值(这个数值提前设置好的),这就需要使用SPP插入多层卷积和全连接层中间。
这就要求我们在使用网络前需要对图像进行一些预处理操作,比如:裁剪(crop)、拉伸(warp)等。但是裁剪会丢失信息,拉伸会把图片拉得不像之前的样子(w i d e),都会产生一些问题。SPP就是来解决这些问题的。
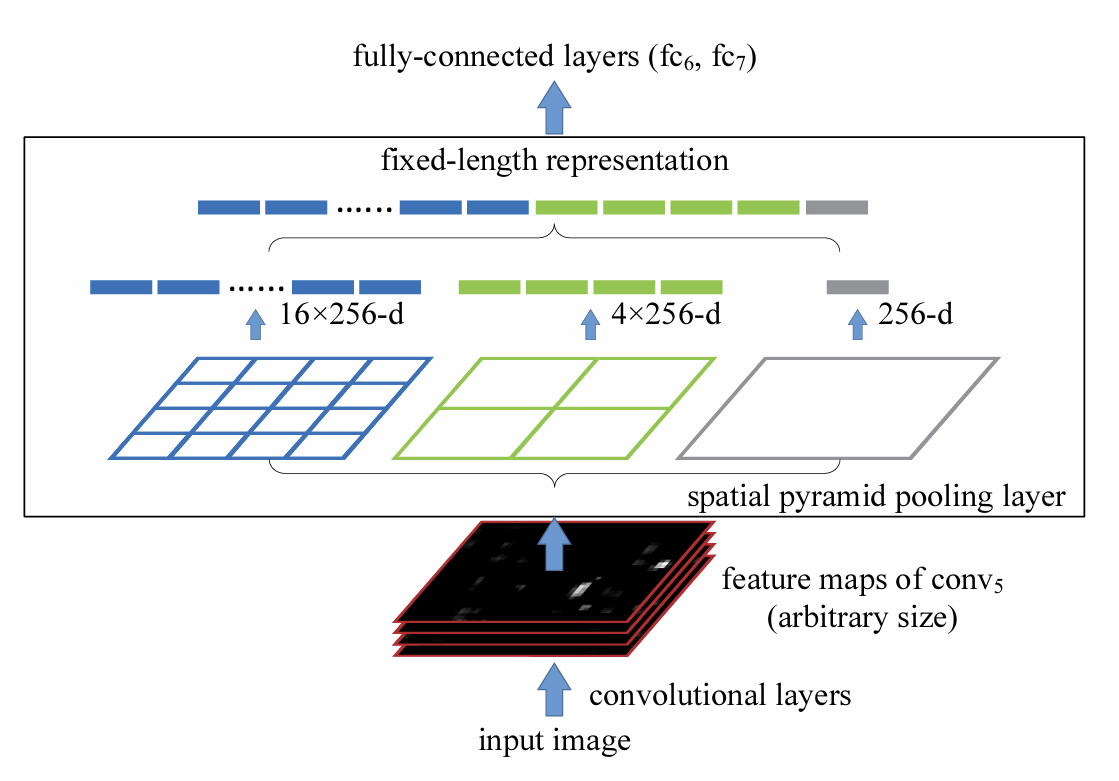
SPP的核心在于使用多个不同尺寸sliding window pooling(上图中的蓝色 $4 \times 4$、青色 $2 \times 2$、灰色 $1 \times 1$ 窗口)对上层(卷积层)获得的feature maps 进行采样(池化,文中使用最大池化),将分别得到的结果进行合并就会得到固定长度的输出。通俗的讲,SPP就相当于标准通道层,不管任何大小的图像,我都用一套标准的pool(文中说叫: l-level pyramid)对图像进行池化,最后组合成一列相同大小的特征。
Single-Size Training 计算规则
按照传统CNN网络,对于图像的输入需要一个固定的大小,假设为 $224 \times 224$。
经过五个卷积层后,conv5输出的 feature maps的大小为 $a×a$。在第一步假设输入大小为 $224×224$ 的基础上,feature maps的大小为 $13×13$。
开始使用SPP层插入在conv5层后(对应SPP原理图),SPP层中想要得到一组$n×n$的和的特征(比如SPP原理图中$1×1$、$2×2$、$4×4$……..一旦确定,就固定了),文中举例用的n=3、2、1。想要得到这样的一组特征,就要使用一组sliding window 对conv5层得到的feature maps进行pooling。这里涉及sliding window的大小(win)和步长(str)计算,计算如下:
\[w = \left\lceil a / n \right\rceil,\; t = \left\lfloor a / n \right\rfloor\]主要优点
解决输入图片大小不一造成的缺陷。
由于把一个feature map从不同的尺寸进行pooling特征抽取,再聚合,提高了算法的robust和精度。
图像分类、目标检测都可以用,而且效果很棒。
一定程度上缓解了R-CNN耗时过多等问题。
Feature Pyramid Network (FPN)
论文(CVPR 2017)Feature Pyramid Network
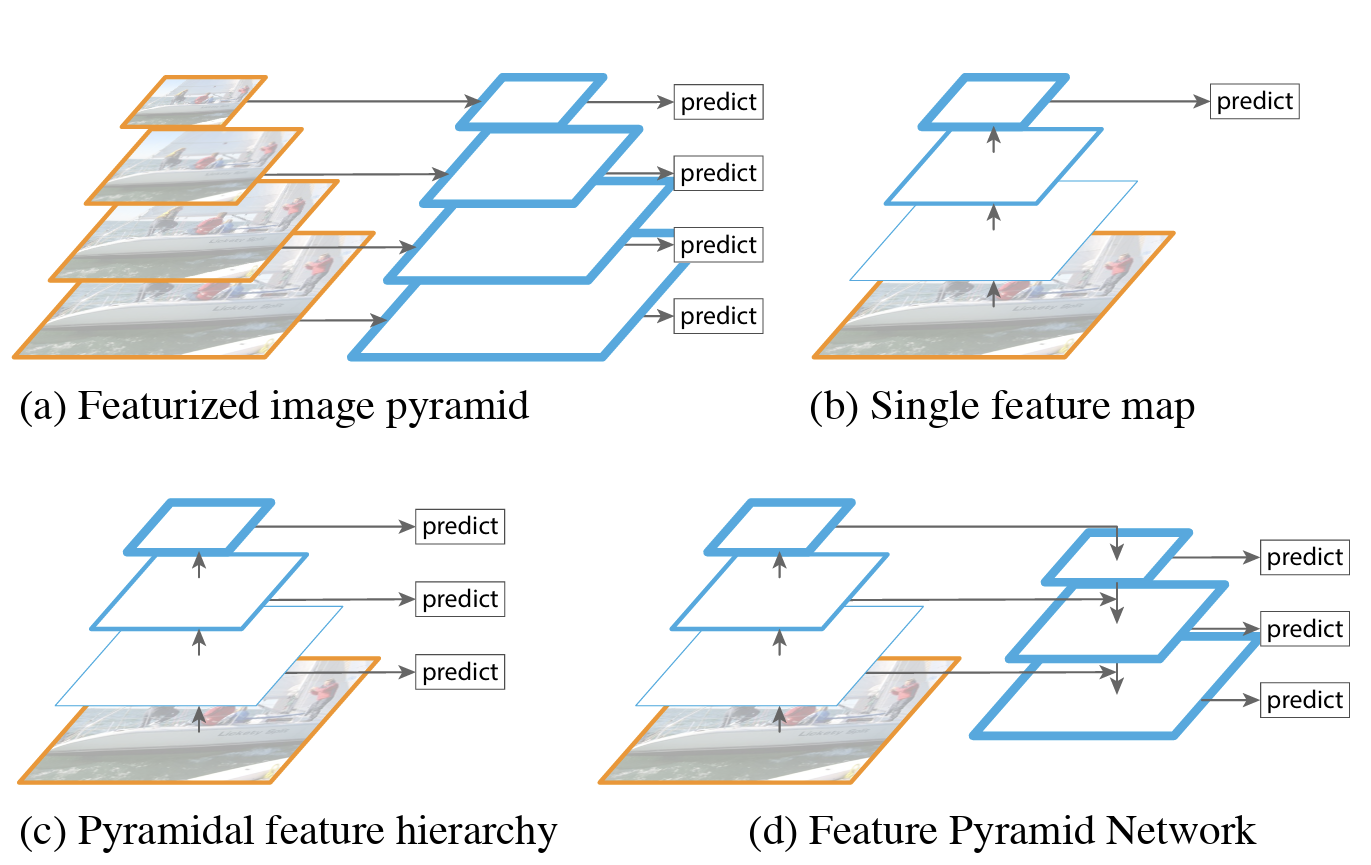
在此之前,目标检测中比较常见的模式有:
Featurized image pyramid:这种方式就是先把图片弄成不同尺寸的,然后再对每种尺寸的图片提取不同尺度的特征,再对每个尺度的特征都进行单独的预测,这种方式的优点是不同尺度的特征都可以包含很丰富的语义信息,但是缺点就是时间成本太高。
Pyramid feature hierarchy:这是SSD采用的多尺度融合的方法,即从网络不同层抽取不同尺度的特征,然后在这不同尺度的特征上分别进行预测,这种方法的优点在于它不需要额外的计算量。而缺点就是有些尺度的特征语义信息不是很丰富,此外,SSD没有用到足够低层的特征,作者认为低层的特征对于小物体检测是非常有帮助的。
Single feature map:这是在SPPnet,Fast R-CNN,Faster R-CNN中使用的,就是在网络的最后一层的特征图上进行预测。这种方法的优点是计算速度会比较快,但是缺点就是最后一层的特征图分辨率低,不能准确的包含物体的位置信息。
所以为了使得不同尺度的特征都包含丰富的语义信息,同时又不使得计算成本过高,作者就采用top down和lateral connection的方式,让低层高分辨率低语义的特征和高层低分辨率高语义的特征融合在一起,使得最终得到的不同尺度的特征图都有丰富的语义信息。
特征金字塔
特征金字塔的结构主要包括三个部分:bottom-up,top-down和lateral connection。
Bottom-up
Bottom-up的过程就是将图片输入到backbone ConvNet中提取特征的过程中。Backbone输出的feature map的尺寸有的是不变的,有的是成2倍的减小的。对于那些输出的尺寸不变的层,把他们归为一个stage,那么每个stage的最后一层输出的特征就被抽取出来。以ResNet为例,将卷积块conv2, conv3, conv4, conv5的输出定义为${C_2, C_3, C_4, C_5}$ ,这些都是每个stage中最后一个残差块的输出,这些输出分别是原图的${1/4,1/8,1/16,1/32}$倍,所以这些特征图的尺寸之间就是2倍的关系。
Top-down
Top-down的过程就是将高层得到的feature map进行上采样然后往下传递,这样做是因为,高层的特征包含丰富的语义信息,经过top-down的传播就能使得这些语义信息传播到低层特征上,使得低层特征也包含丰富的语义信息。本文中,采样方法是最近邻上采样,使得特征图扩大2倍。上采样的目的就是放大图片,在原有图像像素的基础上在像素点之间采用合适的插值算法插入新的像素,在本文中使用的是最近邻上采样(插值)。这是最简单的一种插值方法,不需要计算,在待求像素的四个邻近像素中,将距离待求像素最近的邻近像素值赋给待求像素。
最邻近法计算量较小,但可能会造成插值生成的图像灰度上的不连续,在灰度变化的地方可能出现明显的锯齿状。
Lateral connection
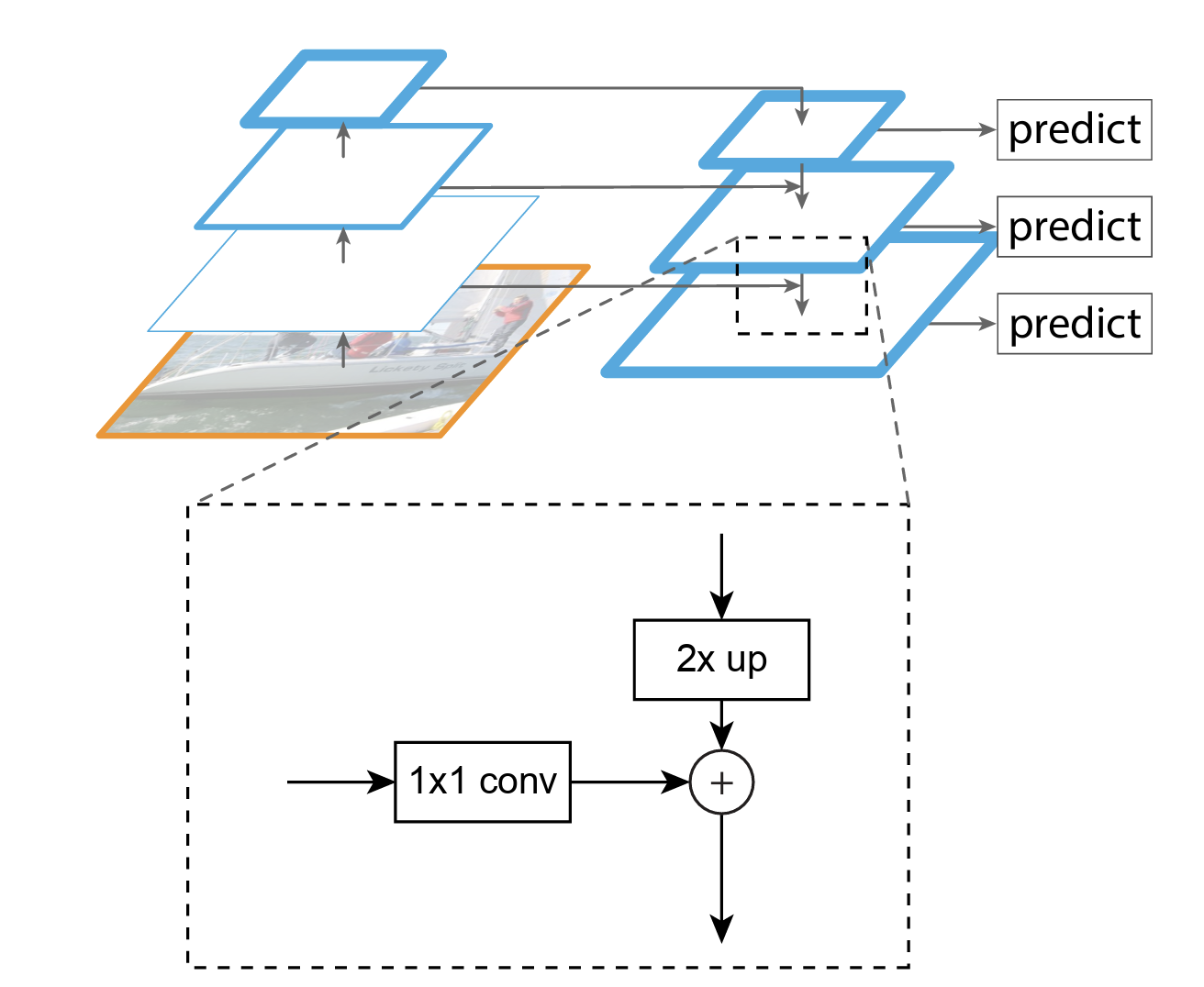
如图所示,lateral connection主要包括三个步骤:
- 对于每个stage输出的feature map $C_n$,都先进行一个1*1的卷积降低维度。
-
然后再将得到的特征和上一层采样得到特征图 $P_{n+1}$ 进行融合,就是直接相加,element-wise addition。因为每个stage输出的特征图之间是2倍的关系,所以上一层上采样得到的特征图的大小和本层的大小一样,就可以直接将对应元素相加 。
- 相加完之后需要进行一个$3 \times 3$的卷积才能得到本层的特征输出$P_n$。使用这个$3 \times 3$卷积的目的是为了消除上采样产生的混叠效应(aliasing effect),混叠效应应该就是指上边提到的‘插值生成的图像灰度不连续,在灰度变化的地方可能出现明显的锯齿状’。在本文中,因为金字塔所有层的输出特征都共享classifiers / regressors,所以输出的维度都被统一为256,即这些 $3\times 3$ 的卷积的channel都为256。
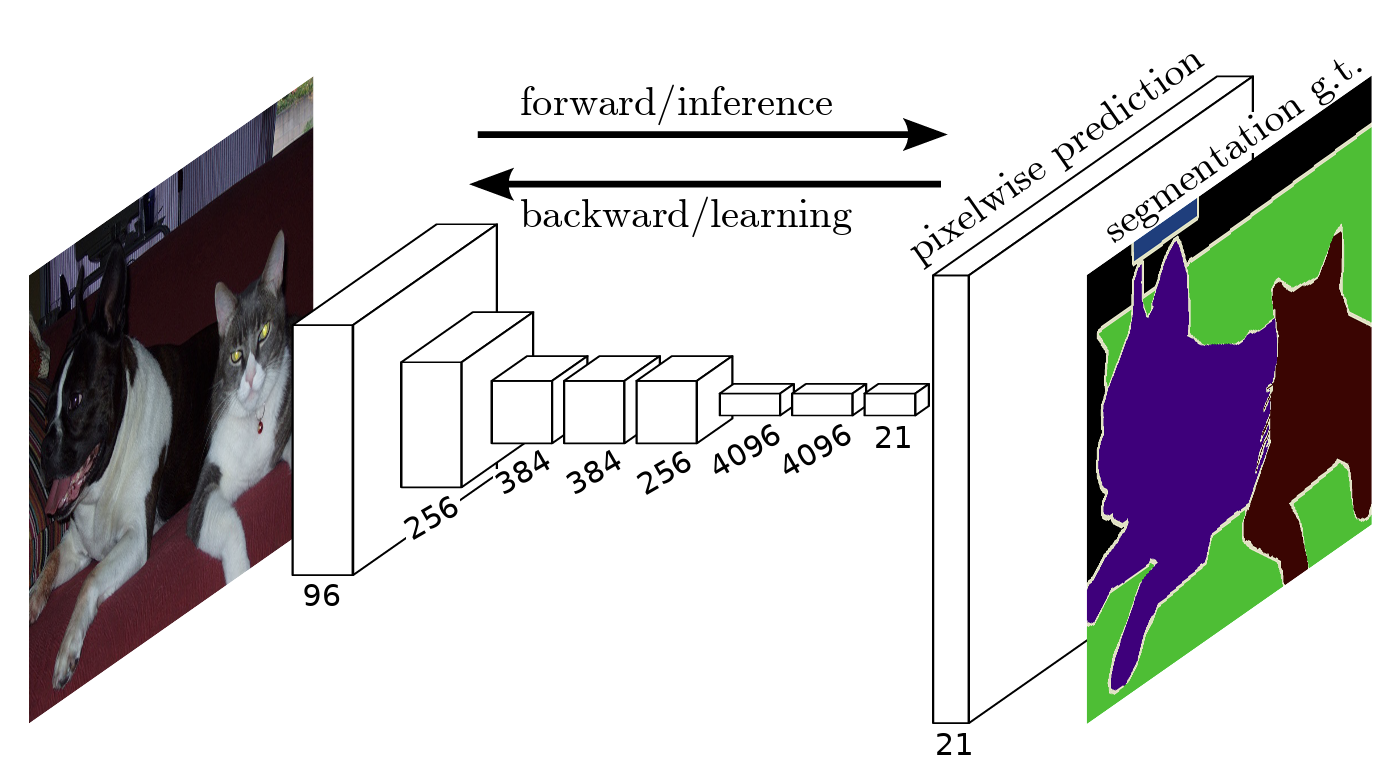
Fully Convolutional Network (FCN)
论文(CVPR 2015)Fully Convolutional Networks for Semantic Segmentation
全卷积网络(fully convolutional network,FCN)采用卷积神经网络实现了从图像像素到像素类别的变换。
CNN与FCN
通常CNN网络在卷积层之后会接上若干个全连接层, 将卷积层产生的特征图(feature map)映射成一个固定长度的特征向量。以AlexNet为代表的经典CNN结构适合于图像级的分类和回归任务,因为它们最后都期望得到整个输入图像的一个数值描述(概率),然后用softmax得到结果就可以了。
FCN对图像进行像素级的分类,从而解决了语义级别的图像分割(semantic segmentation)问题。FCN可以接受任意尺寸的输入图像,采用反卷积层对最后一个卷积层的feature map进行上采样, 使它恢复到输入图像相同的尺寸,从而可以对每个像素都产生了一个预测, 同时保留了原始输入图像中的空间信息, 最后在上采样的特征图上进行逐像素分类。最后逐个像素计算softmax分类的损失, 相当于每一个像素对应一个训练样本。
FCN流程
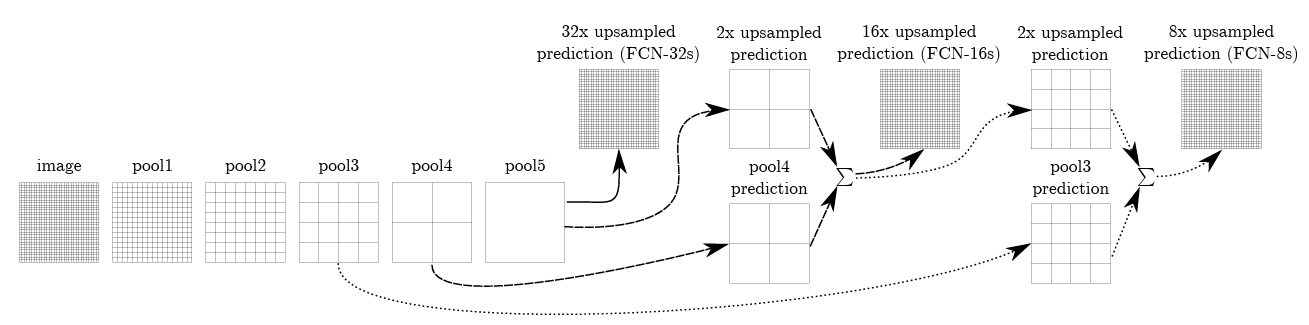
FCN网络的流程如下:
- 首先输入图像,经过pool1,尺寸变为原来尺寸的一半。
- 在经过pool2,尺寸变为原来的1/4。
- 接下来经过pool3、4、5层,大小分别变为原来的1/8、1/16、1/32。
- 经过conv6-7,输出的尺寸依然是原图的1/32。
- FCN-32s最后使用反卷积,使得输出图像的密集程度和原图相同。
- 然后把pool4的特征图拿出来,把conv7的尺寸扩大两倍至原图的1/16,将他俩做融合,再通过反卷积扩大16倍得到原图一样的尺寸。
- 最后将pool3的特征图拿出来,把conv7的尺寸扩大两倍、把conv4的尺寸扩大两倍至原图的1/8,三者融合通过反卷积得到原图尺寸。
“网络结构图下:不难发现FCN网络前面的部分和VGG16结构一样,先是两个卷积一个池化,接两个卷积一个池化,然后跟上三组三个卷积一个池化。最后的全连接层换成了全卷积层。将最后一个全卷积层得到的特征图反卷积,然后反卷积与1/16的特征图拼接,再将得到的特征图反卷积与1/8的特征图拼接,最后反卷积成原图尺寸。”
反卷积-升采样
FCN会先进行上采样,即扩大像素,然后再进行卷积——通过学习获得权值。反卷积层(橙色×3)可以把输入数据尺寸放大。和卷积层一样,上采样的具体参数经过训练确定。