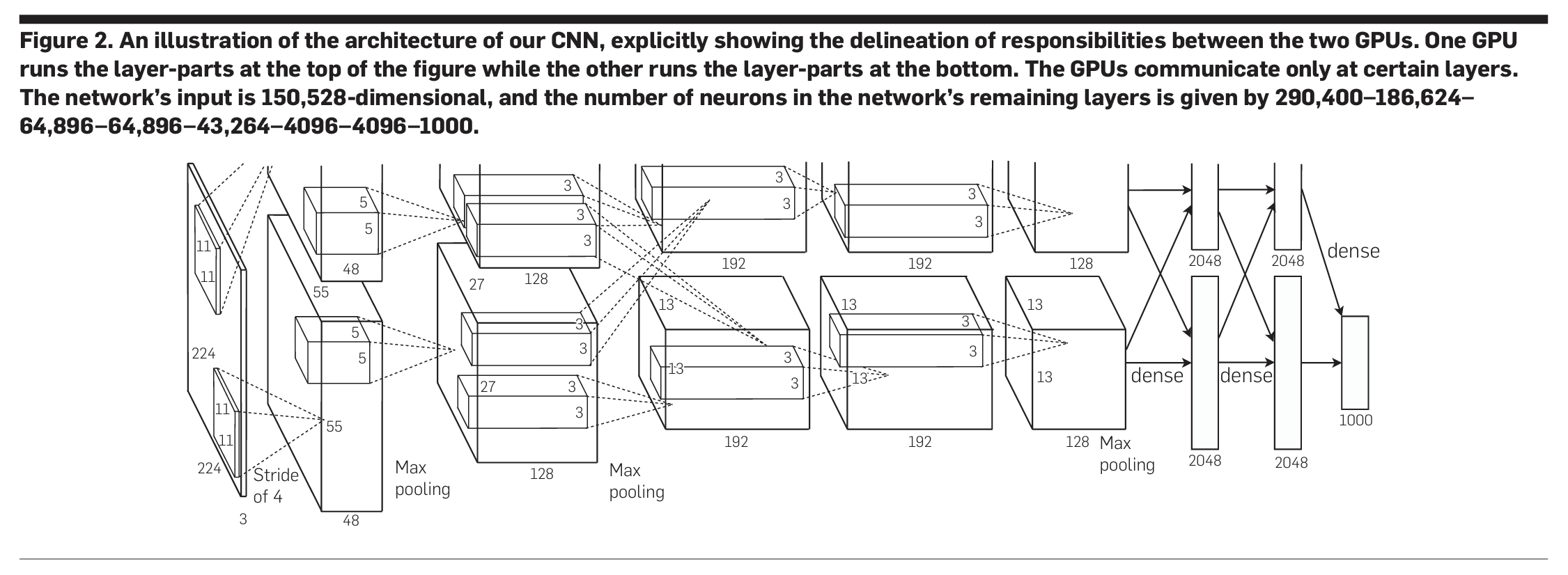
Going Deeper with Convolutions
GoogLeNet, 2014. 是比较早期的工作。
主要贡献
提出深度卷积神经网络结构Inception。
传统的提高神经网络性能的方法:
- 增加深度(
网络层次数量) - 增加宽度(
每一层的神经元数量)
该方案简单、容易但有两个主要的缺点:
- 容易过拟合
尺寸增大则参数数量增加,使网络更容易过拟合,尤其是样本不足的情况下。
- 需要更强的计算能力
过去的解决方式:稀疏连接
稀疏连接有两种方法:
- 空间(
spatial)上的稀疏连接,也就是CNN。其只对输入图像的局部进行卷积,而不是对整个图像进行卷积,同时参数共享降低了总参数的数目并减少了计算量 - 在特征(
feature)维度上的稀疏连接进行处理,也就是在通道的维度上进行处理。
问题:稀疏层计算能力浪费
非均匀的稀疏模型要求更多的复杂工程和计算基础结构,当碰到在非均匀的稀疏数据结构上进行数值计算时,现在的计算架构效率非常低下。
Inception 模块
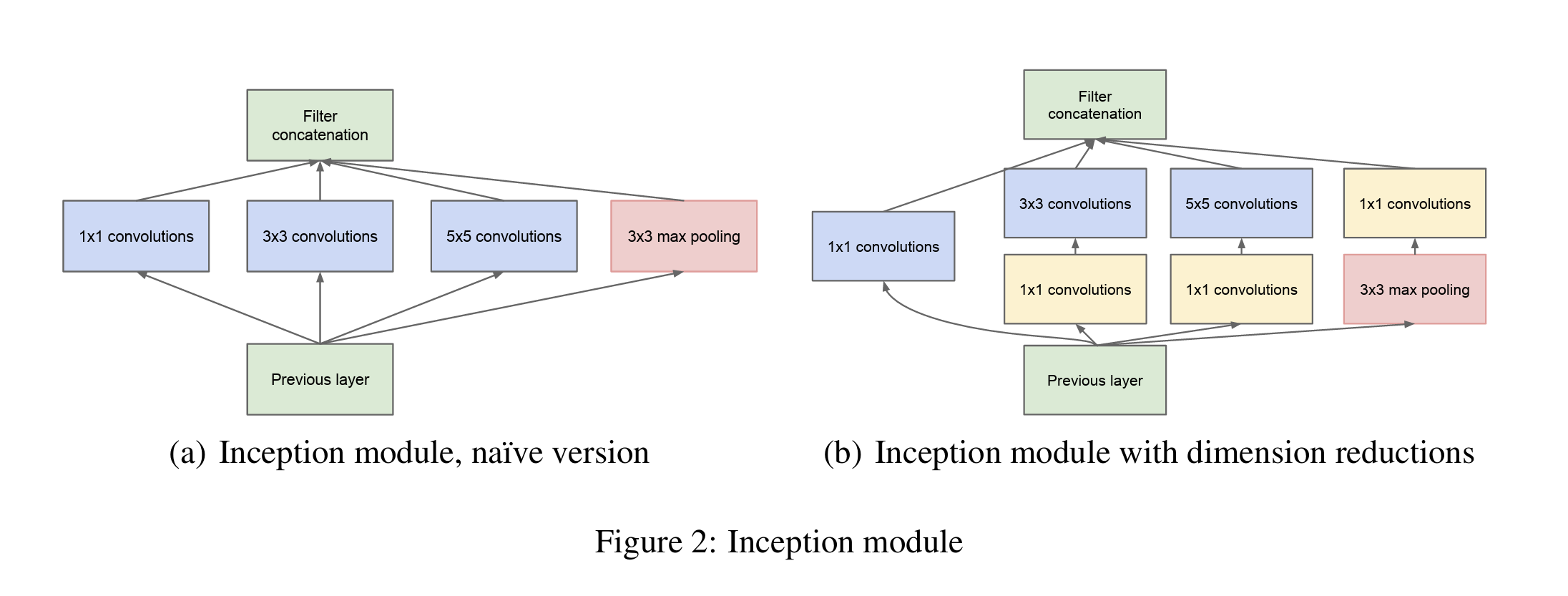
Inception 模块使用不同尺寸的卷积核来提取不同尺度下的feature,再统合在一起。为了降维,引入$1 \times 1$ 卷积(右图)。
不同尺寸的卷积核,可以提取不同尺度的特征,代表不同的相关的特征,并同时引入了多尺度。由于网络的越深层,需要提取更抽象的特征,因此,相应的 $3 \times 3$ 和 $5 \times 5$ 的卷积核数量要相应的增多。
在所有卷积核运算结束之后,通过 concatenate 运算(在 depth 维度上进行),将结果进行组合。整个 GoogLeNet 网络通过大量 Inception 模块堆叠而成。
SSD: Single Shot MultiBox Detector
2016.
目标检测近年来已经取得了很重要的进展,主流的算法主要分为两个类型(参考RefineDet):
- Two stages:以Faster RCNN为代表,即RPN网络先生成proposals目标定位,再对proposals进行classification+bounding box regression完成目标分类。RCNN系列将检测结果分为两部分求解:物体类别(分类问题),物体位置即bounding box(回归问题)。two-stage方法的优势是准确度高。
- Single shot:以YOLO/SSD为代表,一次性完成classification+bounding box regression。其优势是速度快,但是均匀的密集采样的一个重要缺点是训练比较困难,这主要是因为正样本与负样本(背景)极其不均衡(参见Focal Loss),导致模型准确度稍低。
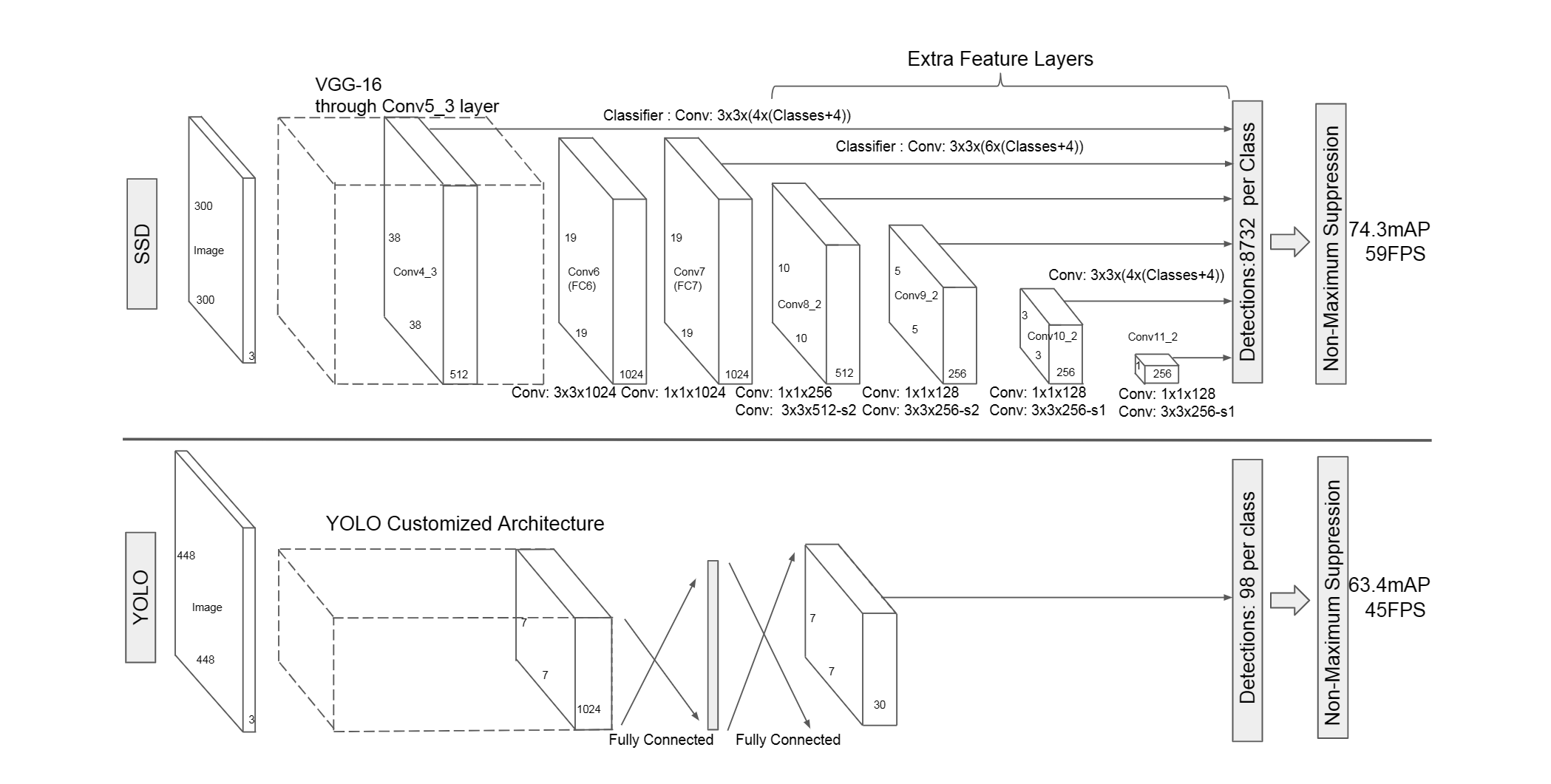
上图:one-stage算法SSD和Yolo
- YOLO在卷积层后接全连接层,即检测时只利用了最高层Feature maps(包括Faster RCNN也是如此)
- SSD采用金字塔结构,即利用了conv4-3/conv-7/conv6-2/conv7-2/conv8_2/conv9_2这些大小不同的feature maps,在多个feature maps上同时进行softmax分类和位置回归
- SSD还加入了Prior box
设计理念
采用多尺度特征图用于检测
所谓多尺度采用大小不同的特征图,CNN网络一般前面的特征图比较大,后面会逐渐采用stride=2的卷积或者pool来降低特征图大小,这正如图3所示,一个比较大的特征图和一个比较小的特征图,它们都用来做检测。这样做的好处是比较大的特征图来用来检测相对较小的目标,而小的特征图负责检测大目标,如图4所示,8x8的特征图可以划分更多的单元,但是其每个单元的先验框尺度比较小。
采用卷积进行检测
与Yolo最后采用全连接层不同,SSD直接采用卷积对不同的特征图来进行提取检测结果。对于形状为 $m \times n \times p$ 的特征图,只需要采用 $3 \times 3 \times p$ 这样比较小的卷积核得到检测值。
设置先验框
在Yolo中,每个单元预测多个边界框,但是其都是相对这个单元本身(正方块),但是真实目标的形状是多变的,Yolo需要在训练过程中自适应目标的形状。而SSD借鉴了Faster R-CNN中anchor的理念,每个单元设置尺度或者长宽比不同的先验框,预测的边界框(bounding boxes)是以这些先验框为基准的,在一定程度上减少训练难度。
训练过程
先验框匹配
在训练过程中,首先要确定训练图片中的ground truth(真实目标)与哪个先验框来进行匹配,与之匹配的先验框所对应的边界框将负责预测它。在Yolo中,ground truth的中心落在哪个单元格,该单元格中与其IOU最大的边界框负责预测它。但是在SSD中却完全不一样,SSD的先验框与ground truth的匹配原则主要有两点。首先,对于图片中每个ground truth,找到与其IOU最大的先验框,该先验框与其匹配,这样,可以保证每个ground truth一定与某个先验框匹配。通常称与ground truth匹配的先验框为正样本(其实应该是先验框对应的预测box,不过由于是一一对应的就这样称呼了),反之,若一个先验框没有与任何ground truth进行匹配,那么该先验框只能与背景匹配,就是负样本。
损失函数
略
数据扩增
其实不是很重要
预测过程
预测过程比较简单,对于每个预测框,首先根据类别置信度确定其类别(置信度最大者)与置信度值,并过滤掉属于背景的预测框。然后根据置信度阈值(如0.5)过滤掉阈值较低的预测框。对于留下的预测框进行解码,根据先验框得到其真实的位置参数(解码后一般还需要做clip,防止预测框位置超出图片)。解码之后,一般需要根据置信度进行降序排列,然后仅保留top-k(如400)个预测框。最后就是进行NMS算法,过滤掉那些重叠度较大的预测框。最后剩余的预测框就是检测结果了。
You Only Look Once: Unified, Real-Time Object Detection
2016.
single-shot 开山之作:YOLO
网络结构
YOLO检测网络包括24个卷积层和2个全连接层,如下图所示。

其中,卷积层用来提取图像特征,全连接层用来预测图像位置和类别概率值。
YOLO网络借鉴了GoogLeNet分类网络结构。不同的是,YOLO未使用inception module,而是使用 $1 \times 1$ 卷积层(此处 $1 \times 1$ 卷积层的存在是为了跨通道信息整合)+ $3 \times 3$ 卷积层简单替代。
YOLO将输入图像分成 $S \times S$ 个格子,每个格子负责检测‘落入’该格子的物体。若某个物体的中心位置的坐标落入到某个格子,那么这个格子就负责检测出这个物体。
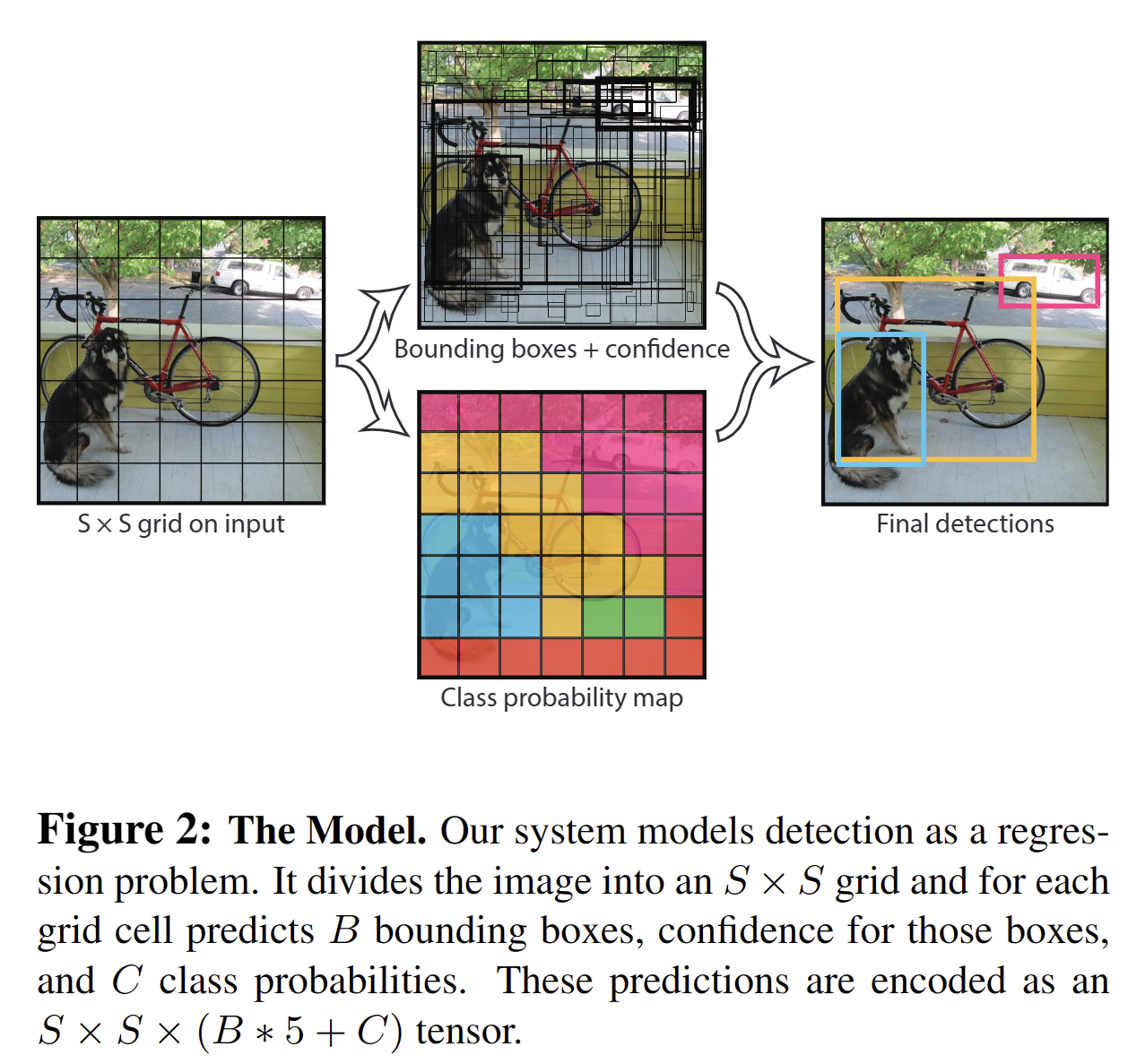
Bounding box信息包含5个数据值,分别是x,y,w,h,和confidence。其中x,y是指当前格子预测得到的物体的bounding box的中心位置的坐标。w,h是bounding box的宽度和高度。注意:实际训练过程中,w和h的值使用图像的宽度和高度进行归一化到[0,1]区间内;x,y是bounding box中心位置相对于当前格子位置的偏移值,并且被归一化到[0,1]。
confidence反映当前bounding box是否包含物体以及物体位置的准确性,计算方式如下:
\[\mathrm{confidence} = \mathrm{P}(object) \times \mathrm{IOU}\]其中,若bounding box包含物体,则$\mathrm{P}(object) = 1$;否则$\mathrm{P}(object) = 0$.
注意:
- 由于输出层为全连接层,因此在检测时,YOLO训练模型只支持与训练图像相同的输入分辨率。
- 虽然每个格子可以预测B个bounding box,但是最终只选择只选择IOU最高的bounding box作为物体检测输出,即每个格子最多只预测出一个物体。当物体占画面比例较小,如图像中包含畜群或鸟群时,每个格子包含多个物体,但却只能检测出其中一个。这是YOLO方法的一个缺陷。
Rich Feature Hierarchies for Accurate Object Detection and Semantic Segmentation
2014.
Birth of R-CNN,不再赘述
Squeeze-and-Excitation Networks
2020.
卷积神经网络(CNN)的核心结构块是卷积算子,卷积算子使网络能够在每一层的局部感受野接收域中融合空间(spatial)和通道(channel)信息来构造信息特征。之前的大量研究已经探究其空间成分,试图通过提高CNN整个特征层次(feature hierarchy)的空间编码(spatial encodings)质量来增强CNN的表征能力。本文将重点放在了通道(channel)关系上,并提出了一种新的结构单元:“Squeeze-and-Excitation” (SE) block,它通过显式建模通道之间的相互依赖性,自适应的重新校准通道方向上的特征响应。将这个SE block推得在一起,就形成了SENet。实验证明,SE块略微增加计算成本的情况下,为现有的最先进的CNN带来了显著的性能提升。
省流:SE block可以看做是为每一个通道上的feature map自适应学习一个权值。然后将它们的信息进行有效整合。
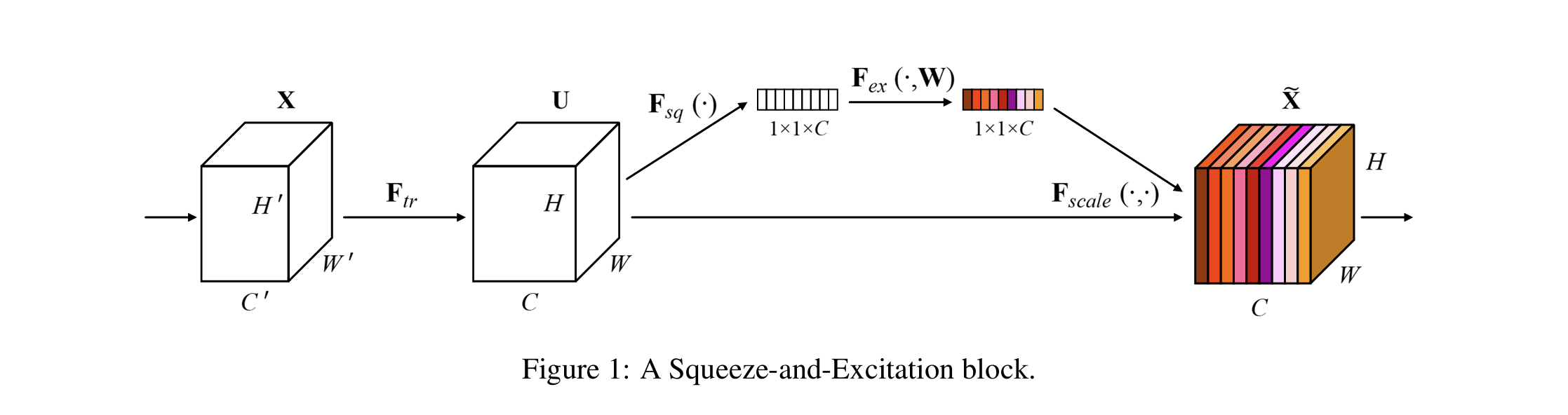
输入 $X \in W^\prime \times H^\prime \times C^\prime $,经过 $F_{tr}$ (卷积操作)输出 $U \in W \times H \times C$。$V = \left[v_1, v_2, \ldots, v_c\right]$ 表示可学习的卷积核集合,其中 $v_c$ 表示第$c$个卷积核参数。输出 $U = \left[u_1, u_2, \ldots, u_c\right]$,即
\[\mathbf{u}_c = \mathbf{v}_c * \mathbf{X} = \sum^{C^\prime}_{s=1}\mathbf{v}_c^s * \mathbf{x}^s\]∗ 表示卷积,$v_c$表示第c个通道的卷积核,X表示输入。 $u_c$表示第c个通道的输出, $u_c$特征图的大小为$H \times W$。为了简化计算,偏置项被忽略。该公式就是常规的卷积操作(nn.Conv())。目的是为了提取特征,以及改变通道数(c’->c),为后续操作提供适当的特征图(U)。
Squeeze: Global Information Embedding
考虑到每一个卷积操作因为其感受野只能获取局部的上下文信息,为了进一步获取全局信息,本文建议将全局空间信息压缩到一个通道描述符中。这一操作通道全局平均池化来实现。
\[z_c = \mathbf{F}_{sq}(\mathbf{u}_c) = \frac{1}{H \times W}\sum^H_{i=1}\sum^{W}_{j=1}\mathbf{u}_c(i, j)\]形式上,统计量 $z_c$ 是按通道缩小U的空间大小来生成的(即C通道特征图的平均值)。$z_c$ 表示第c个统计量,$u_c$ 表示第C通道的特征图,其大小为 $H \times W$。$(i, j)$表示特征图上的该位置的值。那么特征图$U$经过$\mathbf{F}_{sq}(U)$ ,输出一个全局统计向量,大小为 $1\times 1 \times c$。该向量在通道维度聚合全局信息。
Excitation: Adaptive Recalibration
为了利用sq操作中聚合的信息,作者在它之后执行了第二个操作 $\mathbf{F}{ex}$,目的是完全捕获通道方面的依赖性。该部分的作用是通过 $z_c$ 学习每个c(通道)的权重。$\mathbf{F}{ex}$ 要求做到以下三点:
- 要足够灵活(它能够学习通道间的非线性交互),这样能保证学习到的权重值比较具有价值。
- 要足够简单,这样不至于添加SE blocks之后,网络的训练速度大幅度降低。
- 通道之间的关系应该是一种非互斥关系,因为我们想要确保允许强调多个通道。
根据上述要求,excitation部分使用了两层全连接构成的门机制(gate mechanism)。门控单元S(即图1中的1x1xc的特征向量)的计算方式如下:
\[\mathbf{s} = \mathbf{F}_{ex}(\mathbf{z}, \mathbf{W}) = \sigma(g(\mathbf{z}, \mathbf{W})) = \sigma(\mathbf{W}_2\delta(\mathbf{W}_1\mathbf{z}))\]其中 $\delta$ 表示RELU激活函数, $\sigma$ 表示sigmoid激活函数。 $W_1 \in \Re^{\frac{C}{r}\times C}$,$W_2 \in \Re^{\frac{C}{r}\times C}$ 分别是两个全连接层的权值矩阵。 $r$是维度衰减因子。论文中是16,C/r则是中间层的隐层节点数。
得到门控单元 S 后,最后的输出 $\overset\sim{x}$ 表示为 $S$ 和 $U$ 的向量积,即图1中的 $F_{scale}(\cdot,\cdot)$ 操作:
\[\overset\sim{x}_c = \mathbf{F}_{scale}(\mathbf{u}_c, s_c) = s_c\mathbf{u}_c\]其中 $\overset\sim{x}_c$ 是 $\overset\sim{x}$ 某个特征通道的Feature map。 $s_c$ 是门控单元 $s_c$(向量)中的一个标量值。
以上就是SE blocks算法的全部内容。
Deep Residual Learning for Image Recognition
2015.
残差神经网络,之前的文章里已经提到,略
Very Deep Convolutional Networks for Large-Scale Image Recognition
VGGnet (2014)
VGG原理
相比于 LeNet 网络,VGG 网络的一个改进点是将 大尺寸的卷积核 用 多个小尺寸的卷积核 代替。
比如:VGG使用 2个3X3的卷积核 来代替 5X5的卷积核,3个3X3的卷积核 代替7X7的卷积核。
这样做的好处是:
- 在保证相同感受野的情况下,多个小卷积层堆积可以提升网络深度,增加特征提取能力(非线性层增加)。
- 参数更少。比如$1$个大小为$5$的感受野 等价于$2$个步长为$1$,$3 \times 3$大小的卷积核堆叠。(即$1$个$5 \times 5$的卷积核等于$2$个$3 \times 3$的卷积核)。而$1$个$5 \times 5$卷积核的参数量为 $5\times 5\times C^2$。而$2$个$3 \times 3$卷积核的参数量为 $2\times 3\times 3\times C^2$。很显然,$18C^2 < 25C^2$。
- $3 \times 3$卷积核更有利于保持图像性质。
“VGG网络结构非常一致,从头到尾使用3X3的卷积和2X2的max pooling。”
ImageNet Classification with Deep Convolutional Neural Networks
论文中神经网络由卷积层、最大池化层和全连接层组成,激活函数采用了当时全新的Relu,最后使用1000路的softmax作为分类输出,并且使用了“dropout”正则化方法来避免过拟合。