Non-maximum suppression, NMS
非极大值抑制算法(Non-maximum suppression, NMS)是有anchor系列目标检测的标配,是很常见的后续处理步骤。NMS主要用于消除多余的检测框,消除的标准通常是IoU。
大致流程:
-
选取这类box中scores最大的那一个,记为current_box,并保留它(因为它预测出当前位置有物体的概率最大,对于我们来说当前confidence越大说明当前box中包含物体的可能性就越大)
-
计算current_box与其余的box的IOU。如果其IOU大于我们设定的阈值,那么就舍弃这些boxes(由于可能这两个box表示同一目标,因此这两个box的IOU就比较大,会超过我们设定的阈值,所以就保留分数高的那一个)
-
从最后剩余的boxes中,再找出最大scores的那一个(之前那个大的已经保存到输出的数组中,这个是从剩下的里面再挑一个最大的)
-
如此循环往复
循环神经网络 Recurrent Neural Network (RNN)
循环神经网络的重点在于它关注上下文。比如在NLP模型中,如果要对某一个位置上出现的词语进行推理,就需要结合上下文。为了将之前的信息引入到神经网络中(有的时候还需要之后的信息,在后文的双向循环神经网络部分会提到)。
网络结构
o (output)
/|\
V| _
|/ \
s \|/W
/|\_/
U|
|
x (input)
x是一个向量,它表示输入层的值(这里面没有画出来表示神经元节点的圆圈);s是一个向量,它表示隐藏层的值(这里隐藏层面画了一个节点,你也可以想象这一层其实是多个节点,节点数与向量s的维度相同);U是输入层到隐藏层的权重矩阵;o也是一个向量,它表示输出层的值;V是隐藏层到输出层的权重矩阵。那么,现在我们来看看W是什么。循环神经网络的隐藏层的值s不仅仅取决于当前这次的输入x,还取决于上一次隐藏层的值s。权重矩阵W就是隐藏层上一次的值作为这一次的输入的权重。
也就是说,循环神经网络是和时间有关的。
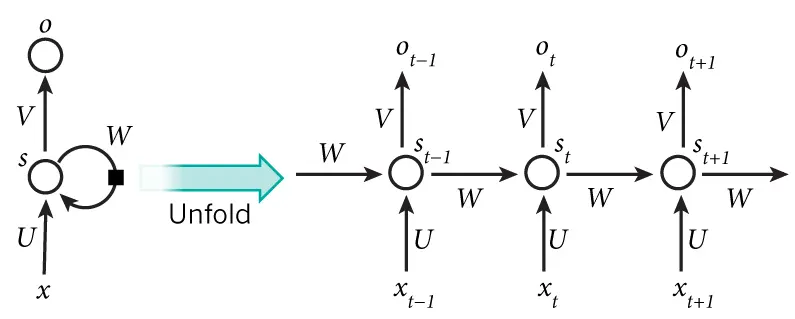
有公式:
\(o_t = g(V_{s_t})\) \(s_t = f(U_{x_t} + W_{s_{t-1}})\)
输出$o_t$是一个全连接层。V是输出层的权重矩阵,g是激活函数。式2是隐藏层的计算公式,它是循环层。U是输入x的权重矩阵,W是上一次的值$s_{t-1}$作为这一次的输入的权重矩阵,f是激活函数。
从上面的公式我们可以看出,循环层和全连接层的区别就是循环层多了一个权重矩阵W。可以发现之前的数值是以等比递减的权重输入当前的隐藏层的。
不断代入可以获得:
\[o_t = g(V_{s_t}) = Vf(U_{x_t} + Wf(U_{x_{t-1}} + Wf(U_{x_{t-2}} + Wf(U_{x_{t-3}} + \cdots ))))\]我们成功地在网络中引入了之前的数据,那么如果要让后续的数据参与训练,该怎么办呢?
答案是双向卷积神经网络。
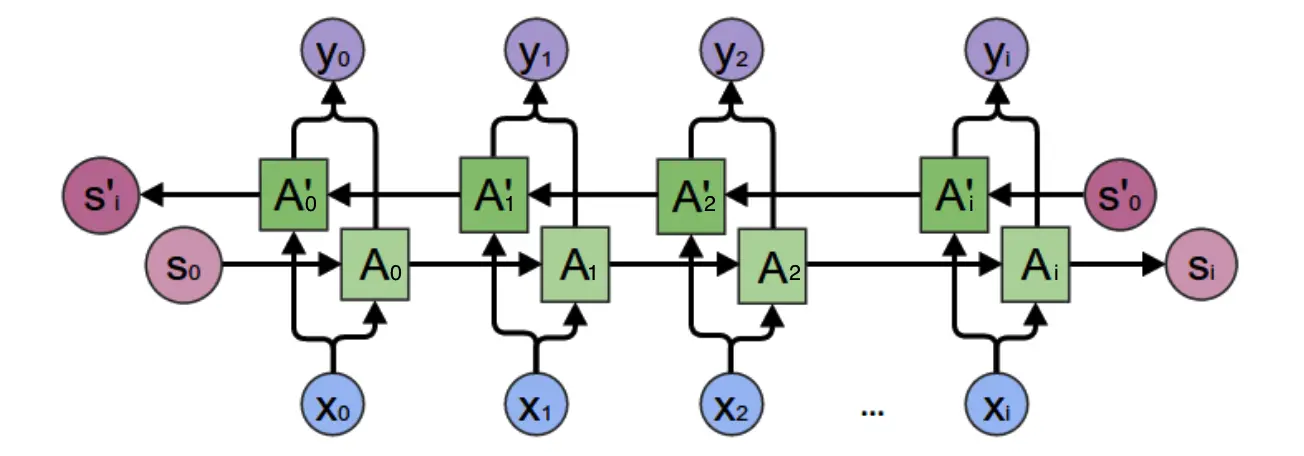
双向卷积神经网络的隐藏层要保存两个值,一个$A$参与正向计算,另一个值$A_t^\prime$参与反向计算。最终的输出$y_t$值取决于$A_t$和$A_t^\prime$。其计算方法为:
\[y_t = g(VA_t + V_t^\prime A_t^\prime)\] \[A_t = f(WA_{t-1} + Ux_t)\] \[A^\prime_t = f(W^\prime A^\prime_{t+1} + U^\prime x_t)\]正向计算时,隐藏层的值与有关;反向计算时,隐藏层的值和$s_t$与$s_{t-1}$有关;最终的输出取决于正向和反向计算的加和。于是有:
\[o_t = g(Vs_t + V^\prime s^\prime_t)\] \[s_t = f(Ux_t + Ws_{t-1})\] \[s^\prime_t = f(U^\prime x_t + W^\prime s^\prime_{t+1})\]正向计算和反向计算不共享权重,也就是说U和U’、W和W’、V和V’都是不同的权重矩阵。
循环神经网络的训练算法:BPTT
BPTT算法是针对循环层的训练算法,它的基本原理和反向传播算法是一样的,也包含同样的三个步骤:
- 前向计算每个神经元的输出值;
- 反向计算每个神经元的误差项值,它是误差函数E对神经元j的加权输入的偏导数;
- 计算每个权重的梯度。
最后再用随机梯度下降算法更新权重。
算法细节和其他细节请阅读此文
长短时记忆网络 Long Short Term Memory Network (LSTM)
LSTM是为了解决RNN的梯度消失问题提出的。在RNN中,由于$w$的指数性质,距离$t$太远的数值难以提供有效的梯度。
长短时记忆网络的思路比较简单。原始RNN的隐藏层只有一个状态,即h,它对于短期的输入非常敏感。那么,假如我们再增加一个状态,即c,让它来保存长期的状态,那么问题不就解决了么?
新增加的状态c,称为单元状态(cell state)。
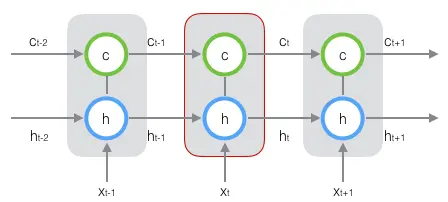
在t时刻,LSTM的输入有三个:当前时刻网络的输入值$\mathbf{x}_t$、上一时刻LSTM的输出值$\mathbf{h}_{t-1}$、以及上一时刻的单元状态$\mathbf{c}_{t-1}$;LSTM的输出有两个:当前时刻LSTM输出值$\mathbf{h}_t$、和当前时刻的单元状态$\mathbf{c}_t$。注意$\mathbf{x}$、$\mathbf{h}$、$\mathbf{c}$都是向量。
LSTM的思路是使用三个控制开关。第一个开关,负责控制继续保存长期状态c;第二个开关,负责控制把即时状态输入到长期状态c;第三个开关,负责控制是否把长期状态c作为当前的LSTM的输出。
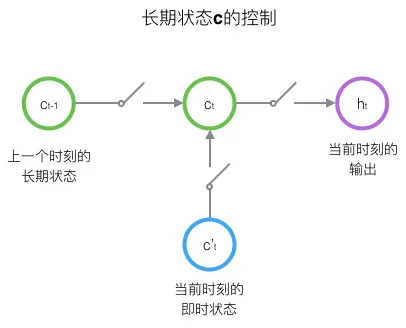
LSTM的前向计算
门实际上就是一层全连接层,它的输入是一个向量,输出是一个0到1之间的实数向量。假设W是门的权重向量,$\mathbf{b}$是偏置项,那么门可以表示为:
\[g(\mathbf{x}) = \sigma(W\mathbf{x} + b)\]因为$\sigma$(也就是sigmoid函数)的值域是(0,1),所以门的状态都是半开半闭的。
LSTM用两个门来控制单元状态c的内容,一个是遗忘门(forget gate),它决定了上一时刻的单元状态$\mathbf{c}_{t-1}$有多少保留到当前时刻$\mathbf{c}_t$;另一个是输入门(input gate),它决定了当前时刻网络的输入$\mathbf{x}_t$有多少保存到单元状态$\mathbf{c}_t$。LSTM用输出门(output gate)来控制单元状态$\mathbf{c}_t$有多少输出到LSTM的当前输出值$\mathbf{h}_t$。
…因为没法花太长时间搬运文字(尤其是敲公式),这里给出原文链接:
Gate Recurrent Unit, GRU
GRU是LSTM的变体。更改在于:
-
将输入门、遗忘门、输出门变为两个门:更新门(Update Gate)和重置门(Reset Gate)。
-
将单元状态与输出合并为一个状态:$\textbf{h}$。
简单示意: 有一个当前的输入 $x^t$,和上一个节点传递下来的隐状态(hidden state)$h^{t-1}$ ,这个隐状态包含了之前节点的相关信息。
结合 $x^t$ 和 $h^{t-1}$,GRU会得到当前隐藏节点的输出 $y^t$ 和传递给下一个节点的隐状态 $h^t$。
y^t
/|\
|
h^{t-1}->GRU->h^t
/|\
|
x^t
递归神经网络 Recursive Neural Network (RNN)
因为神经网络的输入层单元个数是固定的,因此必须用循环或者递归的方式来处理长度可变的输入。循环神经网络实现了前者,通过将长度不定的输入分割为等长度的小块,然后再依次的输入到网络中,从而实现了神经网络对变长输入的处理。一个典型的例子是,当我们处理一句话的时候,我们可以把一句话看作是词组成的序列,然后,每次向循环神经网络输入一个词,如此循环直至整句话输入完毕,循环神经网络将产生对应的输出。如此,我们就能处理任意长度的句子了。
尽管递归神经网络具有更为强大的表示能力,但是在实际应用中并不太流行。其中一个主要原因是,递归神经网络的输入是树/图结构,而这种结构需要花费很多人工去标注。想象一下,如果我们用循环神经网络处理句子,那么我们可以直接把句子作为输入。然而,如果我们用递归神经网络处理句子,我们就必须把每个句子标注为语法解析树的形式,这无疑要花费非常大的精力。很多时候,相对于递归神经网络能够带来的性能提升,这个投入是不太划算的。
前向计算
$\mathbf{c}_1$和$\mathbf{c}_2$分别是表示两个子节点的向量,$\mathbf{p}$是表示父节点的向量。子节点和父节点组成一个全连接神经网络,也就是子节点的每个神经元都和父节点的每个神经元两两相连。我们用矩阵$W表示这些连接上的权重,它的维度将是$d \times 2d$,其中,$d$表示每个节点的维度。父节点的计算公式可以写成:
\[\mathbf{p} = \tanh(W\left[ \begin{matrix}\mathbf{c}_1 \\ \mathbf{c}_2\end{matrix}\right] + \mathbf{b})\]在上式中,$\tanh$是激活函数(当然也可以用其它的激活函数),$\mathbf{b}$是偏置项,它也是一个维度为d的向量。
