写在前面

这篇post还没有动工，最近在忙标数据、整理文书和编译原理作业之类的事情，不过我必须push自己学东西，所以今天就先把文件创建一下（3.25）

好的现在开始学（3.26）

首先看到了一个总集篇，那么我们的文章也根据这个总集篇开始吧。

Denoising Diffusion Probabilistic Models

论文链接

reference 1 reference 2 (强推reference2，讲得很清楚，我这里基本就是搬运一下他的)

Diffusion Model 的开山之作。

扩散概率模型(diffusion probabilistic models)，简称扩散模型(diffusion model)模型的本质是一个马尔可夫链，这个马尔可夫链包括前向过程(forward process / diffusion process)和反向过程(reverse process)，前向过程是有具体的表达式可以计算的，后向过程是利用神经网络来学习的。前向过程存在的意义就是帮助神经网络去训练逆向过程，也即前向过程中得到的噪声就是一系列标签，根据这些标签，逆向过程在去噪的时候就知道噪音是怎么加进去的，进而进行训练。

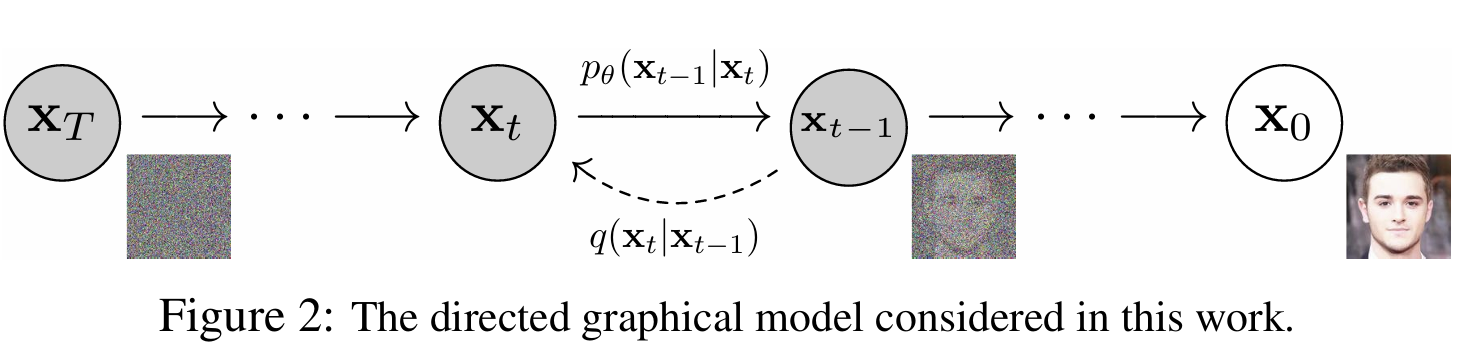
(在图中，后向过程的PDF(概率密度函数)是 $p_{\theta}$，前向过程的则是$q$，我们在后文维持这个符号）

$\mathbf{x}_T$ 表示纯高斯噪声，$\mathbf{x}_0$ 表示生成的样本，因此我们要估计 $\mathbf{x}_0$ 的概率密度函数 $p_{\theta}(\mathbf{x}_0)$。我们可以利用马尔科夫链的性质根据条件概率逐步推导。对概率密度估计的一个经典方法就是最大似然估计，我们将会给出 $p_{\theta}(\mathbf{x}_0)$ 的最大似然估计。

前向过程 Forward Process

前向过程又称扩散过程，其是一个马尔科夫过程(即当前状态只和前一个状态有关)。我们向原始图像 $\mathbf{x}_0$中逐步添加高斯噪声，噪声的标准差是固定值 $\beta_t$ 来确定的，均值是固定值 $\beta_t$ 和 $ t-1$ 时刻的数据 $\mathbf{x}_{t-1}$ 确定的。随着$t$不断增大，最终分布$ \mathbf{x}_T$服从于各向同性的高斯分布了。那么我们要加多少次噪声呢，也即$T$取多大好呢？论文中将$T$看做成一个超参数，$T = 1000$，即加1000次噪声后，$\mathbf{x}_T$会变成各向同性的高斯分布。下方是论文中给出的扩散过程$ \mathbf{x}_t$的分布。

我们可以利用重参数化技巧，将其改写成下面的式子

通过这个式子，我们就可以很直观的看到这个噪声是怎么加的，即 $\sqrt{1 - \beta_t} × \mathrm{Image} + \sqrt{\beta_t} × \mathrm{Noise}$ ，$\mathrm{Image}$ 是前一时刻生成的图像，即上式中的 $\mathbf{x}_{t-1}$；$\mathrm{Noise}$ 是标准正态分布，即上式中 $\mathbf{z}_{t-1}\sim\mathcal{N}(0,\mathbf{I})$ 。并且这里图像和噪音的权重是不断变化的，也即上式中的 $\beta_t$，论文中将其称作扩散率，也是按照超参数处理，$\beta$ 的范围从0.0001逐步增大到0.02。为什么扩散率是逐渐增大的呢，也即为什么噪音所占的比例越来越大呢？可以反过来理解，在加噪声的过程中，扩散率逐渐增大，对应着在去噪声的过程中，扩散率逐渐减小，也就是说，去噪的过程是先把”明显”的噪声给去除，对应着较大的扩散率；当去到一定程度，逐渐逼近真实真实图像的时候，去噪速率逐渐减慢，开始微调，也就是对应着较小的扩散率。

现在我们可以根据 $\mathbf{x}_{t-1}$ 得到 $\mathbf{x}_tx$，那么如果我们给出了原始图像 $\mathbf{x}_0$。能不能通过一次计算就得到加噪任意 $t$ 次之后的 $\mathbf{x}_t$？答案是可以的。

首先令 $\alpha_{t}=1-\beta_{t}$ ，$\bar{\alpha}_{t}=\alpha_1\ast\alpha_2\ast\dots\ast\alpha_{t}$，$\tilde{\mathbf{z}}_{t}\sim\mathcal{N}(0,\mathbf{I})$，则

通过重参数化，我们能得到

以上就是前向过程大概内容，我们从前向过程得到的 $ \mathbf{x}_t$ 将会作为标签，帮助网络学习如何从 $\mathbf{x}_T$ 中一步步去噪，最终得到 $\mathbf{x}_0$ 。

解释：重参数化技巧

如果我们要对高斯分布 $\mathcal{N}(\mu, \sigma^2)$ 进行采样一个噪声 $\epsilon$，等价于先从标准正态分布 $\mathcal{N}(0,1)$ 中采样的到一个噪声 $\mathbf{z}$，然后对其乘上标准差 $\sigma$，加上均值 $\mu$，即 $\epsilon=\mu+\sigma\cdot\mathbf{z}$。举个例子，上面我们已经得到了 $\mathbf{x}_t$ 是从高斯分布 $\mathcal{N}(\sqrt{1-\beta_{t}}\mathbf{x}_{t-1},\beta_{t}\mathbf{I})$ 采样出来的噪声，该高斯分布的均值为 $\sqrt{1-\beta_{t}}\mathbf{x}_{t-1}$ ，标准差为 $\sqrt{\beta_{t}}$ ，所以 $\mathbf{x}_t=\sqrt{1-\beta_{t}}\mathbf{x}_{t-1}+\sqrt{\beta_{t}}\mathbf{z}$。

解释：(*) 处的运算

对于任意两个正态分布 $\mathbf{x}\sim\mathcal{N}(\mu_1,\sigma_1^2)$ 和 $\mathbf{y}\sim\mathcal{N}(\mu_2,\sigma_2^2$，其和的分布 $\mathbf{x}+\mathbf{y}\sim\mathcal{N}(\mu_1+\mu_2,\sigma_1^2+\sigma_2^2)$ 因此对于两个标准正态分布 $\mathbf{z}_{t-2}$ 和 $\mathbf{z}_{t-1}$，将其前面乘上一个系数，$\sqrt{\alpha_{t}-\alpha_{t}\alpha_{t-1}}\mathbf{z}_{t-2}\sim\mathcal{N}(0,\alpha_{t}-\alpha_{t}\alpha_{t-1})$，$\sqrt{1-\alpha_{t}}\mathbf{z}_{t-1}\sim\mathcal{N}(0,1-\alpha_{t})$，因此 $\sqrt{\alpha_{t}-\alpha_{t}\alpha_{t-1}}\mathbf{z}_{t-2}+\sqrt{1-\alpha_{t}}\mathbf{z}_{t-1}\sim\mathcal{N}(0,1-\alpha_{t}\alpha_{t-1})$，也即 $\sqrt{1-\alpha_{t}\alpha_{t-1}}\bar{\mathbf{z}}_{t-2}$。这里不同形式 $ \mathbf{z}$ 单纯起区分作用，本质上都属于标准正态分布 $\mathcal{N}(0,\mathbf{I})$ 的不同采样。

后向过程 Reverse Process

后向过程又称逆扩散过程。我们希望能够从一个噪声分布 $\mathbf{x}_T$ 中逐步去预测出来目标分布 $\mathbf{x}_0$ 。后向过程仍然是一个马尔科夫链过程。根据我们输入的 $\mathbf{x}_{t}$ 去求 $\mathbf{x}_{t-1}$ 的分布，即求 $q(\mathbf{x}_{t-1}\mid\mathbf{x}_{t})$，直接对该公式求解比较困难，可以使用贝叶斯公式将其转化为我们已知的量

由前向过程，$q(\mathbf{x}_{t}\mid\mathbf{x}_{t-1})$ 已知，但是 $q(\mathbf{x}_{t-1})$ 和 $q(\mathbf{x}_{t})$ 未知，但是如果我们给其加上一个先决条件 $q(\mathbf{x}_0)$，也即 $q(\mathbf{x}_{t-1}\mid\mathbf{x}_0)$ 和 $q(\mathbf{x}_{t}\mid\mathbf{x}_0)$，这两个分布由前向过程我们是已知的，所以对 $q(\mathbf{x}_{t-1}\mid\mathbf{x}_{t})$ 加上一个条件 $\mathbf{x}_0$，得到一个多元条件分布

由于扩散过程是马尔科夫过程，所以 $q(\mathbf{x}_{t}\mid\mathbf{x}_{t-1},\mathbf{x}_0)=q(\mathbf{x}_{t}\mid\mathbf{x}_{t-1})$

至此，所有分布我们都已知了，由于正态分布 $\mathcal{N}(\mu,\sigma^2)$ 的概率密度函数 $p(x)=\frac{1}{\sqrt{2\pi}\sigma}\mathrm{e}^{-\frac{1}{2}(\frac{x-\mu}{\sigma})^2}\propto \exp({-\frac{1}{2}(\frac{x-\mu}{\sigma})^2})=\exp(-\frac{1}{2}(\frac{1}{\sigma^2}x^2-\frac{2\mu}{\sigma^2}x+\frac{\mu^2}{\sigma^2}))$，故

• $q(\mathbf{x}_{t}\mid\mathbf{x}_{t-1})=\mathcal{N}(\mathbf{x}_{t};\sqrt{\alpha_{t}}\mathbf{x}_{t-1},(1-\alpha_{t})\mathbf{I})\propto \exp(-\frac{1}{2}\frac{(\mathbf{x}_{t}-\sqrt{\alpha_{t}}\mathbf{x}_{t-1})^2}{1-\alpha_{t}})$
• $\mathbf{x}_{t-1}=\sqrt{\bar{\alpha}_{t-1}}\mathbf{x}_0+\sqrt{1-\bar{\alpha}_{t-1}}\tilde{\mathbf{z}}_{t-1}$ ，利用重参数技巧，则 $q(\mathbf{x}_{t-1}\mid\mathbf{x}_{0})=\mathcal{N}(\mathbf{x}_{t-1};\sqrt{\bar{\alpha}_{t-1}}\mathbf{x}_0,(1-\bar{\alpha}_{t-1})\mathbf{I})\propto \exp(-\frac{1}{2}\frac{(\mathbf{x}_{t-1}-\sqrt{\bar{\alpha}_{t-1}}\mathbf{x}_0)^2}{1-\bar{\alpha}_{t-1}})$
• $\mathbf{x}_{t}=\sqrt{\bar{\alpha}_{t}}\mathbf{x}_0+\sqrt{1-\bar{\alpha}_{t}}\tilde{\mathbf{z}}_{t}$，同样利用重参数技巧，则 $q(\mathbf{x}_{t}\mid\mathbf{x}_{0})=\mathcal{N}(\mathbf{x}_{t};\sqrt{\bar{\alpha}_{t}}\mathbf{x}_0,(1-\bar{\alpha}_{t})\mathbf{I})\propto \exp(-\frac{1}{2}\frac{(\mathbf{x}_{t}-\sqrt{\bar{\alpha}_{t}}\mathbf{x}_0)^2}{1-\bar{\alpha}_{t}})$

这样一来我们对概率分布的运算就可以转化为指数运算。由于对指数进行乘除运算相当于对其系数的加减运算，故

由于我们目标是求与 $\mathbf{x}_{t-1}$ 有关的条件分布，所以将平方项进一步展开化简为关于 $\mathbf{x}_{t-1}$ 的二次函数

这里 $C(\mathbf{x}_t,\mathbf{x}_0)$ 为 $\frac{(\mathbf{x}_{t}-\sqrt{\bar{\alpha}_{t}}\mathbf{x}_0)^2}{1-\bar{\alpha}_{t}}$，也即 $q(\mathbf{x}_t\mid\mathbf{x}_0)$。由于上式是关于 $\mathbf{x}_{t-1}$ 的函数，由于 $q(\mathbf{x}_t\mid\mathbf{x}_0)$ 不含 $\mathbf{x}_{t-1}$，故将其视为常数 $C$。由于 $q(\mathbf{x}_{t-1}\mid\mathbf{x}_{t},\mathbf{x}_0)$ 服从于正态分布，所以我们只需要找到其均值和方差就能求出其分布。怎么求？

现在我们考虑正态分布 $ \mathcal{N}(\mu,\sigma^2)$ 的概率密度函数 $p(x)=\frac{1}{\sqrt{2\pi}\sigma}\mathrm{e}^{-\frac{1}{2}(\frac{x-\mu}{\sigma})^2}\propto \exp({-\frac{1}{2}(\frac{x-\mu}{\sigma})^2})=\exp(-\frac{1}{2}(\frac{1}{\sigma^2}x^2-\frac{2\mu}{\sigma^2}x+\frac{\mu^2}{\sigma^2}))$，所以我们可以找出分布 $q(\mathbf{x}_{t-1}\mid\mathbf{x}_{t},\mathbf{x}_0)$ 的均值和方差。由于方差 $\sigma^2$ 是 $x^2$ 系数的倒数，而 $ \mathbf{x}_{t-1}^2$ 的系数为 $(\frac{\alpha_{t}}{\beta_{t}}+\frac{1}{1-\bar{\alpha}_{t-1}})$ ，其只由人为设置的超参数 $\beta $ 确定，故方差是已知的。$x$ 的系数为 $-\frac{2\mu}{\sigma^2}$，则我们可以根据方差来间接求出均值，$\mathbf{x}_{t-1}$ 的系数为 $(\frac{2\sqrt{\alpha_{t}}}{\beta_t}\mathbf{x}_t+\frac{2\sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}}\mathbf{x}_0)$。可以发现，系数中共有四个变量 $\alpha$，$\beta$，$\mathbf{x}_t$ 和 $\mathbf{x}_0$，其中 $\alpha$，$\beta$，$\mathbf{x}_t$ 都是已知的，但是对于 $\mathbf{x}_0$，由于我们现在是处于后向过程，$\mathbf{x}_0$ 是未知的，现在我们要想办法将 $\mathbf{x}_0$ 用已知量进行替换。我们先将 $\mathbf{x}_{t-1}$ 的均值记为一个关于 $\mathbf{x}_t$ 的函数 $\tilde{\mu}_t(\mathbf{x}_t,\mathbf{x}_0)$。将 $\frac{1}{\sigma^2}=(\frac{\alpha_{t}}{\beta_{t}}+\frac{1}{1-\bar{\alpha}_{t-1}})$ 代入 $\frac{2\mu}{\sigma^2}=(\frac{2\sqrt{\alpha_{t}}}{\beta_t}\mathbf{x}_t+\frac{2\sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}}\mathbf{x}_0)$ 求解可得

现在回想一下，我们已经在前向过程中已经得到了 $\mathbf{x}_0$ 和 $\mathbf{x}_t$ 的关系

现在我们用 $\mathbf{x}_t$ 来表示 $\mathbf{x}_0$

然后将其代入

这样我们就把 $\mathbf{x}_0$ 消掉了，现在我们只要知道了 $\tilde{\mathbf{z}}_t$，就能将 $\tilde{\mu}_t$ 表示出来，进而得到 $q(\mathbf{x}_{t-1}\mid\mathbf{x}_{t},\mathbf{x}_0)$ 的分布，将 $\mathbf{x}_{t-1}$ 采样出来，完成一次去噪过程。那么 $\tilde{\mathbf{z}}_t$ 怎么求呢？

这就要请出深度学习了，我们可以设计一个网络去预测在 $\mathbf{x}_t$ 时刻的噪音 $\tilde{\mathbf{z}}_t$ 。网络的输入是 $\mathbf{x}_t$，网络的输出是 $\tilde{\mathbf{z}}_t$，这是一个预测值，那么真实值在哪呢？我们只有得到真实值，我们才能计算预测值和真值之间的损失，从而训练网络。这时我们考虑前向过程，前向过程中，后一时刻等于前一时刻加上一个噪音 $\mathbf{z}$，$\mathbf{z}$ 是我们采样得来的，是已知的，也就是之前我们所谓的标签。假设我们前向过程由 $\mathbf{x}_{t-1}$ 到 $\mathbf{x}_t$ 加的噪音为 $\mathbf{z}$，那么 $\tilde{\mathbf{z}}_t $ 的真值就是 $\mathbf{z}$，所以我们这个网络训练的 $\tilde{\mathbf{z}}_t$ 就去不断拟合噪声 $\mathbf{z}$。 至此前向过程和后向过程已经介绍结束了。

DDPM算法

训练部分

• 首先在真实图像分布 $q(\mathbf{x}_0)$ 中采样出 $\mathbf{x}_0$，也即我们的训练图像；
• 在区间 $1,…,T$ 中随机生成生成一个 $t$，代表扩散(加噪)次数；
• 从标准正态分布中采样一个随机噪声 $\epsilon$ 计算损失函数，其中的真值是我们刚刚采样得到的噪声 $\epsilon$，网络预测值是 $\epsilon_{\theta}(\sqrt{\bar{\alpha}_t}\mathbf{x}_0+\sqrt{1-\bar{\alpha}_t}\epsilon,t)$，而 $\sqrt{\bar{\alpha}_t}\mathbf{x}_0+\sqrt{1-\bar{\alpha}_t}\epsilon$ 是我们在前向过程中求得的 $\mathbf{x}_t$，这其实可以改写为 $\epsilon_{\theta}(\mathbf{x}_t,t)$，这里的 $t$ 做一个时间编码喂入网络中，因为在后向过程中，每一次迭代的网络都是相同的，即参数共享，那怎么让网络知道现在迭代到哪一步呢，那么我们就将 $t$ 一同传进去参与训练，用 $t$ 来告诉网络我现在进行到第几次迭代了。时间编码和transformer中的位置编码类似。

总结一下，训练过程就是给定 $\mathbf{x}_0$ 和随机噪声 $\epsilon$，然后生成一个扩散(加噪)次数 $t$，进行 $t$ 次扩散过程得到 $\mathbf{x}_t$，然后通过一个网络 $\epsilon_{\theta}$ 来预测一个合适的噪声，也就是 $\tilde{\mathbf{z}}_t$。

采样部分

首先从标准正态分布中采样一个随机噪声 $\mathbf{x}_T$ 。因为我们在前向过程中认为在原图扩散 $T$ 次之后，原图服从于一个各相同性的高斯分布。

然后进行 $T$ 次迭代，对于每一次迭代，首先采样一个标准高斯噪声，但是最后一步就不采样了。然后通过公式计算去噪一次的结果，公式中的 $\epsilon_{\theta}$ 就是我们在训练过程得到的结果。

Denoising Diffusion Implicit Models

论文链接

reference 1 reference 2 (论文翻译)

DDIM和DDPM有相同的训练目标，但是它不再限制扩散过程必须是一个马尔卡夫链，这使得DDIM可以采用更小的采样步数来加速生成过程，DDIM的另外是一个特点是从一个随机噪音生成样本的过程是一个确定的过程（中间没有加入随机噪音）。

在第 3 节中，我们将 DDPM 使用的前向扩散过程（马尔可夫过程）推广到非马尔可夫过程，为此，我们仍然能够设计合适的反向生成马尔可夫链。我们表明，由此得出的变分训练目标有一个相同的替代目标，其刚好就是训练 DDPM 的目标。因此，我们可以从一大类使用相同神经网络的生成模型中自由选择，只需选择不同的非马尔可夫扩散过程（4.1 节）和相应的反向生成马尔可夫链即可。特别是，我们能够使用非马尔可夫扩散过程产生更“短”的生成马尔可夫链（4.2 节），从而可以在更少步中进行模拟。这可以极大地提高生成样本的效率，而在质量方面的只有极小的损失。

在第 5 节中，我们展示了 DDIM 相对于 DDPM 的几个经验优势。首先，当我们使用自己的方法，将采样过程加速 10× 到 100× 时，DDIM 与 DDPM 相比样本生成质量更好。其次，DDIM 样本具有“一致性（consistency）”，而 DDPM 没有；这里“一致性”是指如果我们从相同的初始隐变量开始，并生成多个不同长度马尔可夫链的样本，这些样本会有相似的高级功能。第三，由于 DDIM 中的“一致性”，我们可以通过控制 DDIM 中的初始隐变量来执行语义上有意义的图像插值；这与 DDPM 不同，由于随机生成过程，DDPM 在图像空间附近插值。

Diffusion Models Beat GANs on Image Synthesis

论文链接

reference: 通俗理解 Classifier Guidance 和 Classifier-Free Guidance 的扩散模型

由于数学推导很多，Diffusion这边的论文有点看不懂了，读得有些慢。因此摘要得有些粗略，抱歉——

这篇论文是 OpenAI 的手笔，主要创新点如下：

结构上 (在 Unet 基础上)

We explore the following architectural changes:

• Increasing depth versus width, holding model size relatively constant.
• Increasing the number of attention heads.
• Using attention at $32 \times 32$, $16 \times 16$, and $8 \times 8$ resolutions rather then only at $16 \times 16$.
• Using the BigGAN residual block for upsampling and downsampling the activations.
• Rescaling residual connections with $\frac{1}{\sqrt{2}}$.

classifier-guidance

2021年OpenAI在「Diffusion Models Beat GANs on Image Synthesis」中提出Classifier Guidance，使得扩散模型能够按类生成。后来「More Control for Free! Image Synthesis with Semantic Diffusion Guidance」把Classifier Guidance推广到了Semantic Diffusion，使得扩散模型可以按图像、按文本和多模态条件来生成，例如，风格化可以通过content和style两者共同进行引导，这些都是通过梯度引导来实现。

Classifier Guidance可以通过score function直观地解释，用贝叶斯定理将条件生成概率进行对数分解：

从上式可以看到，Classifier Guidance条件生成只需额外添加一个classifier的梯度来引导。从成本上看，Classifier Guidance 需要训练噪声数据版本的classifier网络，推理时每一步都需要额外计算classifier的梯度。

横向拓展：Classifier-Free Guidance Diffusion

Classifier Guidance 使用显式的分类器引导条件生成有几个问题：一是需要额外训练一个噪声版本的图像分类器。二是该分类器的质量会影响按类别生成的效果。三是通过梯度更新图像会导致对抗攻击效应，生成图像可能会通过人眼不可察觉的细节欺骗分类器，实际上并没有按条件生成。

2022年谷歌提出Classifier-Free Guidance方案，可以规避上述问题，而且可以通过调节引导权重，控制生成图像的逼真性和多样性的平衡，DALL·E 2和Imagen等模型都是以它为基础进行训练和推理。

Classifier-Free Guidance的核心是通过一个隐式分类器来替代显示分类器，而无需直接计算显式分类器及其梯度。根据贝叶斯公式，分类器的梯度可以用条件生成概率和无条件生成概率表示：

把上面的分类器梯度代入到classifier guidance的分类器梯度中可得：

由上可知，新的生成过程不再依赖显示的classifier，因而解决了上述Classifier Guidance的几个问题。

总的来说，训练时，Classifier-Free Guidance需要训练两个模型，一个是无条件生成模型，另一个是条件生成模型。但这两个模型可以用同一个模型表示，训练时只需要以一定概率将条件置空即可。

推理时，最终结果可以由条件生成和无条件生成的线性外推获得，生成效果可以引导系数可以调节，控制生成样本的逼真性和多样性的平衡。

GAN: Generative Adversarial Networks

论文链接

GAN包含有两个模型，一个是生成模型（generative model），一个是判别模型(discriminative model)。生成模型的任务是生成看起来自然真实的、和原始数据相似的实例。判别模型的任务是判断给定的实例看起来是自然真实的还是人为伪造的（真实实例来源于数据集，伪造实例来源于生成模型）。

（等待补充）

VAE: 变分自编码器

（等待补充）

U-Net

论文链接 reference 1

U-Net 是做语义分割用的，它最早被应用于医学影像的细胞级识别。全卷积网络FCN（在之前的CV概念笔记: ResNet, CNN, ROI, RPN, SPP, FPN, FCN (meteorcollector.github.io)有提到过）是它的前辈。

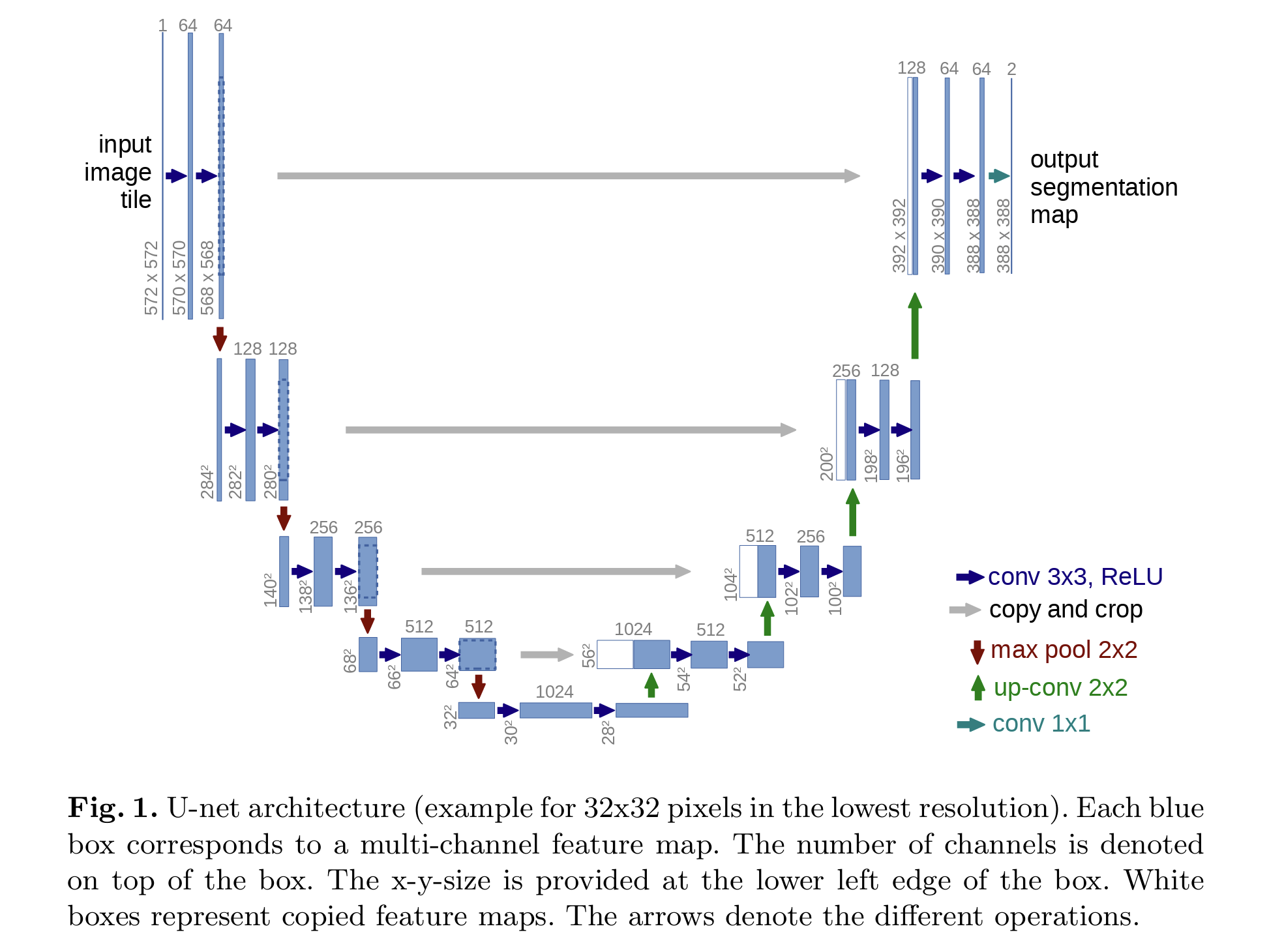
U-Net网络非常简单，前半部分（左边）作用是特征提取，后半部分（右边）是上采样。在一些文献中也把这样的结构叫做Encoder-Decoder结构。因为此网络整体结构类似于大写的英文字母U，故得名U-Net。

（等待补充）