编译原理复习笔记
第三章 词法分析
正则表达式
掌握语法
状态转换图
知道怎么画
DFA, NFA
正则表达式 -> NFA
NFA -> DFA (子集构造法)
DFA最小化 (把所有可区分,即输入某字符去向不同的的状态分开):初始划分 ${S - F, F}$ 其中 $F$ 是终止状态
第四章 语法分析
三板斧:“在进行高效的语法分析之前,需要对文法做以下处理”
消除二义性
二义性的消除方法没有规律可循
消除左递归
消除立即左递归:
$A \to A \alpha_1 \mid \ldots \mid A\alpha_m \mid \beta_1 \mid \ldots \mid \beta_n$
替换为
$A \to \beta_1 A^\prime \mid \ldots \mid \beta_n A^\prime$
$A^\prime \to \alpha_1 A^\prime \mid \ldots \mid \alpha_m A^\prime \mid \varepsilon$
通用算法:
将文法的非终结符号排序为 $A_1, A_2, \ldots , A_n$
for i=1 to n do{
for j=1 to i-1 do {
將形如 A_i -> A_j y 的產生式替換爲 A_i -> b_1 y | b_2 y | ... | b_k y,
其中 A_i -> b_1 | b_2 | ... | b_k 是以 A_i 為左部的所有產生式
}
消除 A_i 的立即左遞歸
}
提取左公因子
这是因为当两个产生式具有相同前缀时无法预测,所以要提取左公因子。
对于每个非终结符号 $A$,找出它的两个或者多个可选产生式体之间的最长公共前缀
例子
S -> i E t S e S | i E t S | a
E -> b
转化为
S -> i E t S S' | a
S' -> e S | \epsilon
E -> b
自顶向下的语法分析
自顶向下分析 缺点:回溯;优点:实现简单;
预测分析技术:确定性、无回溯;FIRST FOLLOW 集计算
FIRST集合和FOLLOW集合
FIRST易得
FOLLOW:首先将右端结束标记 $ 加入 FOLLOW(S) 中,按照以下两个规则不断迭代:
- 如果存在产生式 $A \to \alpha B \beta$,那么 FIRST($\beta$) 中所有非 $\varepsilon$ 的符号都加入 FOLLOW($B$) 中
- 如果存在产生式 $A \to \alpha B$ 或者 $A \to \alpha B \beta$ 包含 $\varepsilon$,那么 FOLLOW($A$) 中所有符号都加入 FOLLOW($B$) 中
例题:第四章PPT P46
LL(1) 预测分析表构造算法
对于文法 $G$ 的每个产生式 $A \to \alpha$
- 对于 FIRST($\alpha$) 中的每个终结符号 $a$,将 $A \to \alpha$ 加入到 $M[A, a]$ 中
- 如果 $\varepsilon$ 在 FIRST($\alpha$),那么对于 FOLLOW($A$) 中的每个符号 $b$,将 $A \to \alpha$ 也加入到 $M[A, b]$ 中
最后在所有的空白条目中填入 error
若预测分析表出现冲突,这个文法是二义的。
自底向上的语法分析
通用框架:移入-归约 (shift-reduce)
简单LR技术 (SLR)、LR技术 (LR)
句柄
如果 $S \underset{rm}{\Rightarrow} \alpha A w \underset{rm}{\Rightarrow} \alpha \beta w$,那么紧跟 $\alpha$ 之后的 $\beta$ 就是 $A \to \beta$ 的一个句柄
在一个最右句型中,句柄右边只有终结符号
移入-归约冲突:不知道是否应该归约
归约-归约冲突:不知道按照什么产生式进行归约
LR语法分析技术
L 表示最左扫描,R 表示反向构造出最右推导,k 表示最多向前看 k 个符号
LR(0)
增广文法
$G$ 的增广文法 $G^\prime$ 是在 $G$ 中增加新开始符号 $S^\prime$,并加入产生式 $S^\prime \to S$ 而得到的
项集闭包
项是文法的一个产生式加上在其中某处的一个点
如果 $I$ 是文法 $G$ 的一个项集,CLOSURE($I$) 这样构造:
- 将 $I$ 中各项加入 CLOSURE($I$)
- 如果 $A \to \alpha \cdot B \beta$ 在 CLOSURE($I$) 中,而 $B \to \gamma$ 是一个产生式,且项 $B \to \cdot \gamma$ 不在 CLOSURE($I$) 中,就将该项加入其中,不断应用该规则直到没有新项可加入
GOTO函数
$I$ 是一个项集,$X$ 是一个文法符号,则 $GOTO(I, X)$ 定义为 $I$ 中所有形如 $[A \to \alpha \cdot X \beta]$ 的项所对应的项 $[A \to \alpha X \cdot \beta]$ 的集合的闭包
LR(0) 项集规范族
从初始项集开始,不断计算各种可能的后继,直到生成所有的项集
LR(0)自动机:第四章 PPT p81
在移入后,根据原来的栈顶状态可以知道新的状态
在规约时,根据规约产生式的右部长度弹出相应状态,也可以根据此时的栈顶状态知道新的状态 P86
SLR 语法分析表
P91 P94
- $[A \to \alpha \cdot a \beta ]$ 在 $I_i$ 中,且 $GOTO(I_i, a) = I_i$,则 $ACTION[i, a]$ = “移入$j$”
- $[A \to \alpha \cdot]$ 在 $I_i$ 中,那么对 $FOLLOW(A)$ 中所有 $a$ ,$ACTION[i, a]$ = “按 $A \to \alpha$ 归约”
- 如果 $[S^\prime \to S\cdot]$ 在 $I_i$ 中,那么将 $ACTION[i, $]$ 设为“接受”
- 如果 $GOTO(I_i, A) = I_j$ ,那么在 $GOTO$ 表中,$GOTO[i, A] = j$
- 空白条目设为 error
SLR
SLR分析器在LR(0)分析器的基础上进一步使用Follow集来解决潜在的移入-归约冲突,从而提高了识别文法的能力。
(可是LR(0)分析表里也涉及了 FOLLOW 啊?LR(0)的语法分析表和SLR的语法分析表有什么区别?)
LR(1) 项集规范族族
向前看一个字符。具体构建过程见 PPT 107 页附近,其中 LR(1) 项集族的构造和 LR(0) 项集族类似,但是 CLOSURE 和 GOTO 有所不同
- 在 CLOSURE 中,当由项 $[A \to \alpha \cdot B \beta, a]$ 生成新项 $[B \to \cdot \theta, b]$ 时,$b$ 必须在 FIRST($\beta a$) 中
- 对 LR($1$) 项集中的任意项 $[A \to \alpha \cdot B \beta, a]$ ,总有 $a$ 在 FOLLOW($A$) 中
LR(1) 语法分析表
与 LR(0) 完全相仿。
LALR分析技术
寻找具有相同核心的 LR(1) 项集,并把它们合并成为一个项集
合并后不会有移入-归约冲突,但是可能会有归约-归约冲突。如果产生了冲突,则该文法不是 LALR 的
第五章 语法制导的翻译
Syntax Directed Translation
经典例题:“n进制”
语法制导的定义 Syntax-Directed Definition SDD 是上下文无关文法和属性/规则的结合
综合属性 synthesized atttribute
- 结点 N 的属性值由 N 的产生式所关联的语义规则来定义
- 通过 N 的子节点或 N 本身的属性值来定义
继承属性 inherited attribute
- 结点 N 的属性值由 N 的父节点所关联的语义规则来定义
- 依赖于 N 的父节点、N 本身和 N 的兄弟结点上的属性值
只包含综合属性的 SDD 称为 S属性 的 SDD,S属性的SDD可以和LR语法分析器一起实现
语义规则不应该有复杂的副作用,不影响其他属性的求值。没有副作用的 SDD 称为 属性文法 (attribute grammar)
L属性的SDD 要么是综合属性,要么是继承属性
自顶向下方式:从根开始,对于每个非终结符号 A,其所对应过程的参数为继承属性,返回值为综合属性
抽象语法树 Abstract Syntax Tree
每个结点代表一个语法结构,对应于运算符;节点的每个子结点代表其子结构,对应于运算分量
示例(属性 E.node 指向 E 对应的抽象语法树的根节点)
| 产生式 | 语义规则 |
|---|---|
| E -> E1 + T | E.node = new Node(‘+’, E1.node, T.node) |
| E -> E1 - T | E.node = new Node(‘-‘, E1.node, T.node) |
| E -> T | E.node = T.node |
| T -> E | T.node = E.node |
| T -> id | T.node = new Leaf(id, id.entry) |
| T -> num | T.node = new Leaf(num, num.val) |
可以发现这样的文法是有左递归的,在自顶向下分析时会发生问题。在消除左递归时,SDT也要进行转换。
不涉及属性值时
| 原始的产生式 | 转换后得到 |
|---|---|
| E -> E_1 + T { print(‘+’); } E -> T |
E -> T R R -> + T { print(‘+’); } R R -> $\varepsilon$ |
涉及属性值时
| 原始的产生式 | 转换后得到 |
|---|---|
| A -> A1 Y { A.a = g(A1.a, Y.y) } A -> X { A.a = f(X.x) } |
A -> X { R.i = f(X.x) } R { A.a = R.s } R -> Y { R.i = g(R.i, Y.y) } R1 { R.s = R1.s } R -> $\varepsilon$ { R.s = R.i } |
第六章 中间代码生成
表达式的有向无环图:指示公共子表达式
三地址代码
- 运算/赋值:x = y op z x = op y
- 复制指令:x = y
- 无条件转移指令:goto L
- 条件转移指令:if x goto L if False x goto L if x relop y goto L
- 过程调用/返回:param x call p, n (调用过程p,n为参数个数)
- 带下标的复制指令:x = y[i] x[i] = y
- 地址/指针赋值:x = &y x = *y *x = y
实际实现时,可以选择以下几种形式
四元式 Quadruple
格式:op arg1 arg2 result
单目运算符不使用 arg2,param运算不使用 arg2 和 result,条件/非条件转移将目标标号放在result字段
三元式 Triple
格式:op arg1 arg2
使用三元式的位置来引用三元式的运算结果,在做题时往往是表格中的编号
x[i] = y 和 x = y[i] 需要拆分为两个三元式,需要先求出带下标一项的地址
间接三元式 Indirect Triple
包含了一个指向三元式的指针的列表
静态单赋值 SSA
所有赋值都是针对具有不同名字的变量,使用很多变量
SDT
ppt里介绍了多种 SDT,分别由计算 T 的类型和宽度的 SDT、声明序列的SDT(维护符号表)、将表达式翻译成三地址代码的 SDD、数组元素的寻址
作业里涉及了数组元素的寻址,其他的没有涉及
类型检查和转换
控制流语句的翻译
继承属性:
-
B.true:B为真时的跳转目标
-
B.false:B为假时的跳转目标
-
S.next:S执行完毕时的跳转目标
注意这些继承属性在传递时不可以颠倒
| 产生式 | 语义规则 |
|---|---|
| P -> S | S.next = newlabel() P.code = S.code || label(S.next) |
| S -> assign | S.code = assign.code |
| S -> if (B) S1 | B.true = newlabel() B.false = S1.next = S.next S.code = B.code || label(B.true) || S1.code |
| S -> if (B) S1 else S2 | B.true = newlabel() B.false = newlabel() S.code = B.code || label(B.true) || S1.code || gen(‘goto’, S.next) || label(B.false) || S2.code |
| S -> while (B) S1 | begin = newlabel() B.true = newlabel() B.false = S.next S.code = label(begin) || B.code || label(B.true) || S1.code || gen(‘goto’, begin) |
| S -> for(S1; B; S2)S3 | B.true = newlabel() B.false = S.next S1.next = newlabel() S2.next = S1.next S3.next = newlabel() S.code = S1.code || label(S1.next) || B.code || label(B.true) || S3.code || label(S3.next) || S2.code || gen(‘goto’, S1.next) |
| S -> S1 S2 | S1.next = newlabel() S2.next = S.next S.code = S1.code || label(S1.next) || S2.code |
布尔表达式
| 产生式 | 语义规则 |
|---|---|
| B -> B1 || B2 | B1.true = B.true // 短路 B1.false = newlabel() B2.true = B.true B2.true = B.false B.code = B1.code || label(B.false) || B2.code |
| B -> B1 && B2 | B1.true = newlabel() B1.false = B.false // 短路 B2.true = B.true B2.false = B.false B.code = B1.code || label(B.true) || B2.code |
| B -> !B1 | B1.true = B.false B1.false = B.true B.code = B1.code |
| B -> E1 rel E2 | B.code = E1.code || E2.code || gen(‘if’ E1.addr rel.op E2.addr ‘goto’ B.true) || gen(‘goto’, B.false) |
| B -> true | B.code = gen(‘goto’ B.true) |
| B -> false | B.code = gen(‘goto’ B.false) |
布尔表达式的回填翻译
作业九有涉及,把抽象语法树画了出来。但是应该不是重点?
| 产生式 | 语义规则 |
|---|---|
| B -> B1 || M B2 | backpatch(B1.falselist, M.instr); B.truelist = merge(B1.truelist, B2.truelist); B.falselist = B2.falselist; |
| B -> B1 && M B2 | backpatch(B1.truelist, M.instr); B.truelist = B2.truelist; B.falselist = merge(B1.falselist, B2.falselist); |
| B -> !B1 | B.truelist = B1.falselist B.falselist = B1.truelist |
| B -> (B1) | B.truelist = B1.truelist B.falselist = B1.falselist |
| B -> E1 rel E2 | B.truelist = B1.makelist(nextinstr) B.falselist = B1.makelist(nextinstr + 1); gen(‘if’ E1.addr rel.op E2.addr ‘goto _’); gen(‘goto _’) |
| B -> true | B.truelist = makelist(nextinstr); gen(‘goto _’); |
| B -> false | B.falselist = makelist(nextinstr); gen(‘goto _’); |
| M -> $\varepsilon$ | M.instr = nextinstr; |
break / continue / switch
暂略
第七章 运行时刻环境
存储分配
| 代码区 |
|---|
| 静态区 |
| 堆区 |
| $\downarrow$ 空闲内存 $\uparrow$ |
| 栈区 |
- 静态分配:编译器在编译时刻就可以做出存储分配决定,不需要考虑程序运行时刻的情形。涉及全局常量 、 全局变量
- 动态分配:栈式存储 :和过程的调用 返回同步进行分配和回收,值的生命期与过程生命期相同 堆存储 :数据对象比创建它的过程调用更长寿。涉及手工进行回收/垃圾回收机制
运行时刻栈要求会画
经典例题:

答案:
高地址
+----------------+-+- 代码区起始
| main的代码 | |
+----------------+ |
| mul的代码 | |
+----------------+ |
| ... |-+- 代码区结束,静态数据区起始
+----------------+ |
| m=100 | |
+----------------+ |
| ... | |
+----------------+-+- 静态数据区结束,动态数据区起始
| | |
+----------------+ | <- SP
| res=200 | |
+----------------+ |
| 0x100 | |
+----------------+ |
| mul返回地址 | |
+----------------+ |
| 200 | |
+----------------+ |
| a=10 | |
+----------------+ |
| b=20 | |
+----------------+ | <- BP
| ... | |
+----------------+-+- 动态数据区结束
| 0x100 |
+----------------+
低地址
这里的栈生长方向可能与常见的不同,考试的时候会指定。
垃圾回收方法
引用计数垃圾回收
对象分配时,引用计数设为1
参数传递时,引用计数加1
引用赋值时,u=v,u指向的对象引用减1,v指向的对象引用加1
过程返回时,局部变量指向对象的引用计数减1
如果一个对象的引用计数为0,在删除对象之前,此对象中各个指针所指对象的引用计数减1
优点:不会引起停顿,也能及时回收垃圾
缺点:开销较大,无法解决循环依赖的垃圾
基于跟踪的垃圾回收
不在垃圾产生是回收,而是周期性地运行,缺点是清扫时系统会被挂起
- 标记-清扫式垃圾回收 1) 标记:从根集开始,跟踪并标记处所有的可达对象;2) 清扫:遍历整个堆区,释放不可达对象。其实就是一个有向图遍历。
- 标记并压缩垃圾回收 1) 标记:标记所有可达对象;2) 计算新位置;3) 移动并设置新的引用。把可达对象移动到堆区的一端,另一端是空闲空间;空闲空间合并成单一块,提高分配内存时的效率。
- 拷贝垃圾回收 堆空间被分为两个半空间(semispace),应用程序在某个半空间内分配存储,当充满这个半空间时,开始垃圾回收。回收时,可达对象被拷贝到另一个半空间;回收完成后,两个半空间角色对调。优点:不涉及任何不可达对象;缺点:必须移动所有可达对象。
开销:标记-清扫式与堆区中存储块的数目成正比;标记并压缩与堆区中存储块的数目和可达对象的总大小成正比;拷贝垃圾回收与可达对象的总大小成正比
第八章 代码生成
IR -> 机器代码 PPT P7附近
基本块
基本块确定方法:确定首指令(leader)
- 第一个三地址指令
- 任意一个转移指令的目标指令
- 紧跟在一个转移指令之后的指令
每个首指令对应于一个基本块,每个基本块都是从首指令开始到下一个首指令之前。
确定基本块中的活跃性、后续使用
初始状态,基本块B中所有非临时变量都是活跃的
从B的最后一个语句开始反向扫描
对于每个语句 i: x = y + z
- 令语句 i 和 x、y、z 的当前活跃性信息/使用信息关联
- 设置 x 为“不活跃”和“无后续使用”
- 设置 y 和 z 为“活跃”,并指明它们的下一次使用设置为语句 i
最后获得各个语句 i 上变量在基本块中的活跃性、后续使用信息
循环
- 循环 $L$ 是一个结点集合
- 存在一个循环入口 (loop entry)结点,是唯一的前驱可以在循环 $L$ 之外的结点,到达其余结点的路径必然先经过这个入口结点
- 其余结点都存在到达入口结点的非空路径,且路径都在$L$中
DAG图
顺序扫描各三地址指令,进行如下处理
- 指令 x = y op z
- 为该指令建立结点 N ,标号为 op ,令 x 和 N 关联
- N 的子结点为 y 和 z 当前 关联的结点
- 指令 x = y
- 假设 y 关联到 N ,那么 x 现在也关联到 N
- 从数组取值的运算 x = a[i] 对应于 =[] 的结点
- 这个结点的左右子节点是数组初始值 a0 和下标 i
- 变量 x 是这个节点的标号之一
- 对数组赋值的运算 a[j] = y 对应于 []= 的结点
- 这个结点的三个子结点分别表示 a0、j 和 y
- 杀死之前所有依赖于 a0 的变量
- 指针赋值 *q = y 对任意变量赋值,杀死全部其他结点
PPT P31 P35 P38 有例子
getReg,冗余代码消除,控制流优化
没找到什么例题啊,复习课上有这么一道:
ST a, R1 LD R1, a 能不能省略?如果在同一个基本块里就可以
感觉优化的大头在第九章?(不过这道题是机器代码,应该还是第八章)
寄存器分配和指派
寄存器分配表:在第十二次作业中有,但是当时写错了,已在md里更正。第十二次作业也有循环识别的问题,当时也做错了。一定要注意定义!
注意寄存器不够的时候记得把变量存到内存;如果变量在出口处活跃,一定要在最后ST回内存!
考试时候可能寄存器少(比如2个)
第九章 机器无关的优化
全局公共子表达式
如果 E 在某次出现之前必然已经被计算过且 E 的运算分量在该次计算之后没有被改变,那么 E 的本次出现就是一个公共子表达式 (common subexpression)
复制传播
PPT里没有严格的定义,在lab的实现中,使用的是后向传播数据流算法
死代码消除
如果一个变量在某个程序点上的值可能会在之后被使用,那么这个变量在这个点上 活跃 (live);否 则这个变量就是 死的 (dead),此时对该变量的赋值就是没有用的死代码
循环不变表达式
循环的同义词运行的不同迭代中表达式的值不变,往往把它们外提
归纳变量强度削减
若某个变量每次都赋值为归纳变量的线性组合,可以把赋值改为增量操作进行强度削减
归纳变量消除*
直接把归纳变量删除,只留下被赋值的变量。PPT里没有提及,但是第十二次作业中出现了
数据流分析
正向数据流分析:$\mathrm{OUT}[s] = f_s(\mathrm{IN}[s])$
逆向数据流分析:$\mathrm{IN}[s] = f_s(\mathrm{OUT}[s])$
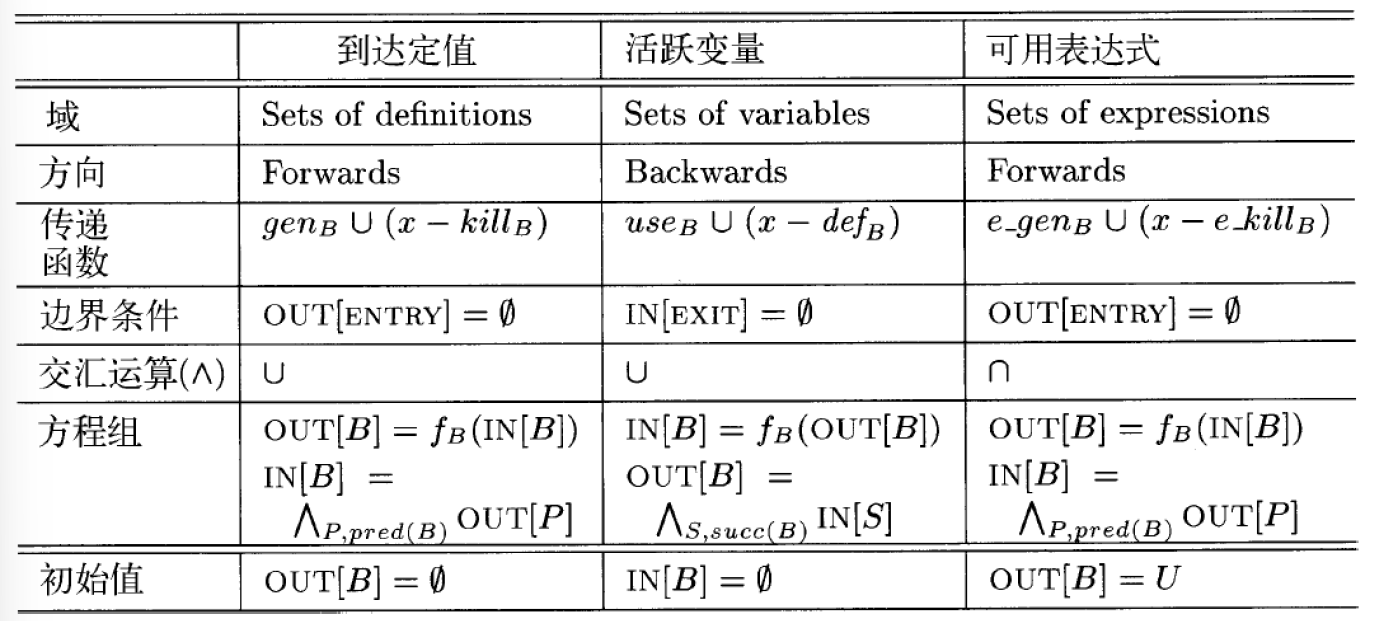
到达定值分析
到达定值分析的gen和kill
对于定值 $d: u - v + w$,它生成了对变量 $u$ 的定值 $d$,杀死其他对 $u$ 的定值。即
$gen_d = \{d\}$,$kill_d = \{\text{程序中其他对$u$的定值}\}$
对于整个基本块
$gen_B = gen_n \cup (gen_{n-1} - kill_n) \cup \ldots \cup (gen_1 - kill_2 - kill_3 - \ldots - kill_n)$
$kill_B = kill_1 \cup kill_2 \cup \ldots \cup kill_n$
$gen_B$ 是被第 $i$ 个语句生成,且没有被其后的句子杀死的定值的集合:向下可见 (downwards exposed)
$kill_B$ 为被 $B$ 各个语句杀死的定值的并集
到达定值分析的控制流方程
$\mathrm{OUT[ENTRY]} = \emptyset$
$\mathrm{OUT[B]} = gen_B \cup (\mathrm{IN[B]} - kill_B)$
$\mathrm{IN[B]} = \cup_{P \in pred(B)} \mathrm{OUT[P]}$
输出结果是表达式的 bitmap
活跃变量分析
活跃变量分析的def和use
对于语句 $s: x = y + z$,$use_s = \{y, z\}$,$def_s = \{x\} - \{y, z\}$
假设基本块中包含语句 $s_1, s_2, \ldots, s_n$ 那么
$use_B = use_1 \cup (use_2 - def_1) \cup (use_3 - def_1 - def_2) \cup \ldots \cup (use_n - def_1 - def_2 - \ldots - def_{n-1})$
$def_B = def_1 \cup (def_2 - use_1) \cup (def_3 - use_1 - use_2) \cup \ldots \cup (def_n - use_1 - use_2 - \ldots - use_{n-1})$
活跃变量分析的数据流方程
$\mathrm{IN[EXIT]} = \emptyset$
$\mathrm{IN[B]} = use_B \cup (\mathrm{OUT[B]} - def_B)$
$\mathrm{OUT[B]} = \cup_{S \in succ(B)} \mathrm{IN[S]}$
可用表达式分析
(用于寻找全局公共子表达式)
- 初始化 $S = \emptyset$
- 从头到尾逐个处理基本块中的指令 $x = y + z$
- 把 $y + z$ 添加到 $S$ 中
- 从 $S$ 中删除任何涉及变量 $x$ 的表达式
- 遍历结束时得到基本块生成的表达式集合
- 杀死的表达式集合:表达式的某个分量在基本块中被定值,并且该表达式没有被再次生成
可用表达式分析的数据流方程
$\mathrm{OUT[ENTRY]} = \emptyset$
$\mathrm{OUT[B]} = e\_gen_B \cup (\mathrm{IN[B]} - e\_kill_B)$
$\mathrm{IN[B]} = \cap_{P \in pred(B)} \mathrm{OUT[P]}$
总结
注意做题的时候,到达定值往往使用bitmap,活跃变量和可用表达式分析则直接写出集合。
部分冗余消除*
即提取全局公共子表达式使其只计算一次,以及循环不变代码外提等技术
懒惰代码移动*
使表达式的计算尽量靠后以利于寄存器的分配
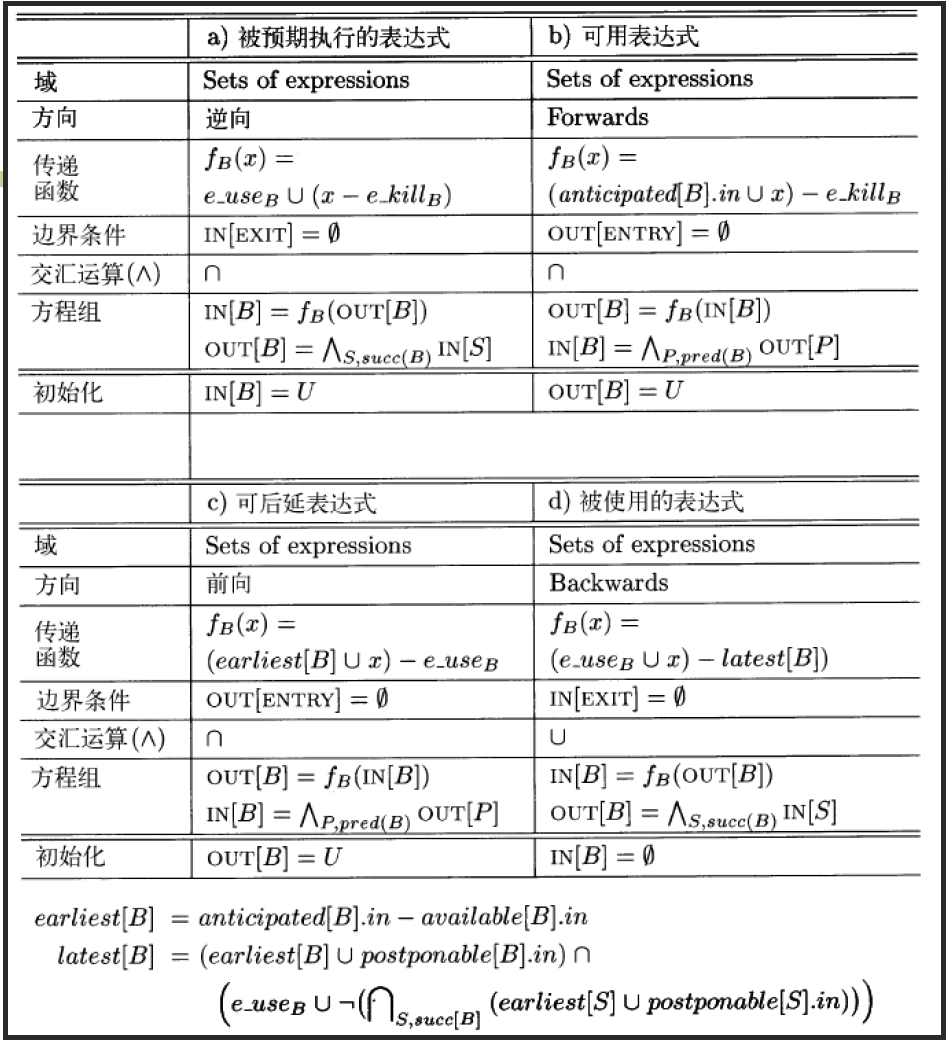
这里作业和重点里都没有涉及,但是ppt里还是有篇幅的…
支配结点树
即支配树。
定义支配 (dominate):如果每条从入口结点到达 $n$ 的路径都经过 $d$ ,那么 $d$ 支配 $n$ ,记为 $d \;\mathrm{dom}\;n$
定义直接支配结点 (immediate dominator):从入口结点到达 $n$ 的任何路径 (不含$n$) 中,它是路径中最后一个支配 $n$ 的结点
$n$ 的直接支配结点 $m$ 具有如下性质:如果 $d \neq n$ 且 $d\;\mathrm{dom}\;n$ ,那么 $d\;\mathrm{dom}\;m$
支配结点也可以用数据流求解,见下:

初始条件:$\mathrm{OUT[ENTRY] = ENTRY}$,$\mathrm{OUT[B] = \text{全集}}$
回边
边 $a \to b$ 存在,但是 $b\;\mathrm{dom}\;a$
自然循环 Natual Loop
性质:有一个唯一的入口结点,即循环头(header),这个结点支配循环中的所有结点。必然存在进入循环头的回边。
定义:给定回边 $n \to d$ 的自然循环是 $d$,加上不经过 $d$ 就能够到达 $n$ 的结点的集合,$d$ 是这个循环的头
构造算法:初始将 $d$ 标记为 visited,从 $n$ 开始逆向对流图进行dfs,把所有访问到的结点加入 loop 集合,标记为 visited。搜索过程中不越过标记为 visited 的结点。loop集合初始值为 ${n, d}$
